Funciones cóncavas y convexas

Función convexa

Una función $f(x)$ se dice convexa en un intervalo $[a, b]$ si, para todo punto $x_0 \in [a, b]$, su gráfica sobre $[a, b]$ queda situada por encima de la recta tangente en $(x_0, f(x_0))$.

Función cóncava

Una función $f(x)$ se dice cóncava en un intervalo $[a, b]$ si, para todo punto $x_0 \in [a, b]$, su gráfica sobre $[a, b]$ queda situada por debajo de la recta tangente en $(x_0, f(x_0))$.

En las secciones siguientes explicaré cómo identificar si una función es cóncava o convexa, ya sea observando su gráfica o analizando sus derivadas.

Cómo reconocer la concavidad o convexidad de una función

Dada una función definida en un intervalo $[a, b]$ y un punto $x_0$ dentro de él, podemos clasificarla así:

• Convexa, si su gráfica en $[a, b]$ se encuentra por encima de la tangente en $(x_0, f(x_0))$
  
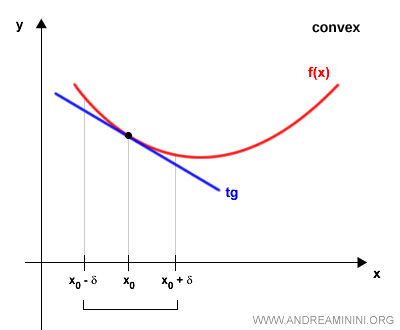
• Cóncava, si su gráfica en $[a, b]$ se encuentra por debajo de la tangente en $(x_0, f(x_0))$
  

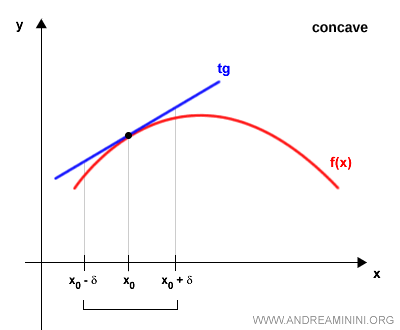
Una función puede ser cóncava o convexa en todo su dominio, o solo en ciertos tramos.

De hecho, es muy frecuente que una misma función sea cóncava en algunos intervalos y convexa en otros.

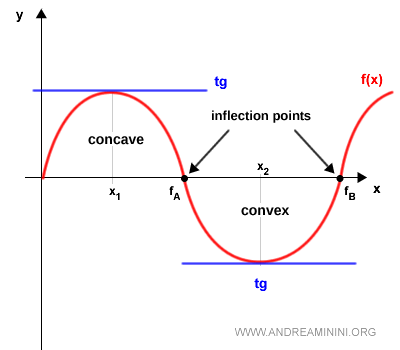
El paso de concavidad a convexidad (y viceversa) se produce en los llamados puntos de inflexión.

¿Qué son los puntos de inflexión?

Un punto de inflexión se da en $x_0$ cuando la recta tangente queda por debajo de la curva a la izquierda de $x_0$ y por encima a la derecha, marcando así la transición de convexa a cóncava o al contrario.

Por ejemplo, en la gráfica siguiente el punto $f_A$ es un punto de inflexión donde la función pasa de cóncava a convexa.

A la izquierda de $f_A$, la curva (en rojo) está por debajo de la tangente (en azul). A la derecha de $f_A$, se sitúa por encima.

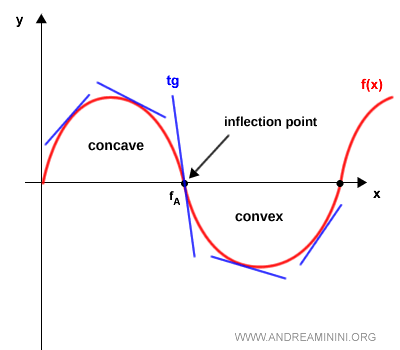
También puede ocurrir el caso opuesto.

Si la tangente está por debajo de la curva a la izquierda de $x_0$ y por encima a la derecha, entonces $x_0$ vuelve a ser un punto de inflexión, pero esta vez señalando la transición de convexa a cóncava.

Por ejemplo, en el punto $f_B$ de la gráfica inferior la función cambia de convexa a cóncava.

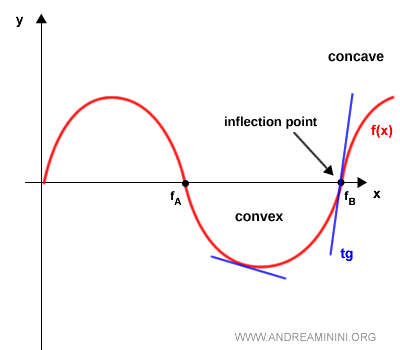
En este caso, la curva (en rojo) está por debajo de la tangente (en azul) antes de $f_B$, y por encima después.

Criterios de concavidad y convexidad

Se puede determinar si una función es convexa o cóncava sin mirar su gráfica, analizando únicamente sus derivadas.

Criterio de convexidad

Si la primera derivada $f'(x)$ es creciente en un intervalo $[a, b]$, la función $f(x)$ es convexa en dicho intervalo. De manera equivalente, la función es convexa si su segunda derivada es no negativa: $$ f''(x) \ge 0 \quad \forall x \in (a, b) $$

En otras palabras, que $f'(x)$ sea creciente equivale a que $f''(x) \ge 0$.

$$ f''(x) \ge 0 $$

Aplicando el criterio de monotonía a la primera derivada, se obtiene que $f''(x)$ es no negativa siempre que $f'(x)$ sea creciente:

$$ f''(x) \ge 0 \quad \Leftrightarrow \quad f'(x)\ \text{es creciente} $$

Ejemplo

La función $f(x) = x^2$ es convexa en $x = 0$, pues su primera derivada $f'(x) = 2x$ es creciente en un entorno de $x = 0$.

Como $f'(x)$ es creciente, se cumple que $f''(x) \ge 0$ cerca de $x = 0$.

Esto confirma que la función es convexa en $x = 0$, ya que cualquier tangente en ese punto queda por debajo de la curva.

Criterio de concavidad

Si la primera derivada $f'(x)$ es decreciente en un intervalo $[a, b]$, la función $f(x)$ es cóncava en dicho intervalo. En otras palabras, $f(x)$ es cóncava si su segunda derivada es no positiva: $$ f''(x) \le 0 \quad \forall x \in (a, b) $$

De nuevo, que $f'(x)$ sea decreciente equivale a afirmar que $f''(x) \le 0$:

$$ f''(x) \le 0 $$

Por tanto, aplicando el criterio de monotonía a $f'(x)$, tenemos:

$$ f''(x) \le 0 \quad \Leftrightarrow \quad f'(x)\ \text{es decreciente} $$

Ejemplo

La función $f(x) = \log x$ es cóncava en $x = 3$, ya que su primera derivada $f'(x) = 1/x$ es decreciente en un entorno de $x = 3$.

Como $f'(x)$ es decreciente, se cumple que $f''(x) \le 0$ cerca de $x = 3$.

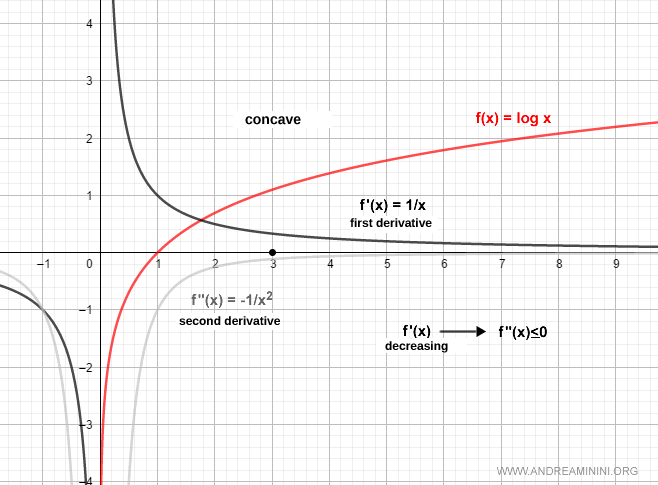
Esto confirma que la función es cóncava en $x = 3$, pues en ese punto la tangente queda por encima de la curva.

Demostración de los criterios de convexidad y concavidad

La demostración consta de dos pasos:

1. Si $f(x)$ es convexa, entonces $f'(x)$ es creciente.
2. Si $f'(x)$ es creciente, entonces $f(x)$ es convexa.

Nota: El criterio de concavidad se obtiene de forma análoga.

Demostración - Parte 1

Supongamos que $f(x)$ es convexa. Queremos probar que $f'(x)$ resulta creciente.

Sea $f(x)$ definida en $[a, b]$, y tomemos dos puntos $x_1 < x_2$ dentro de este intervalo.

Por convexidad, la gráfica de $f(x)$ queda siempre por encima de la tangente en $x_1$ y en $x_2$:

$$ f(x) \ge f(x_1) + f'(x_1)(x - x_1) $$

$$ f(x) \ge f(x_2) + f'(x_2)(x - x_2) $$

para todo $x \in [a, b]$.

Nota: El segundo miembro corresponde a la recta tangente en $x_1$ o en $x_2$.

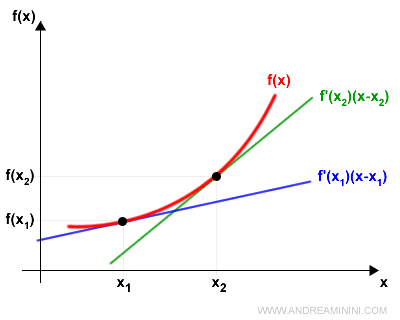
Evaluamos ahora la primera desigualdad en $x = x_2$ y la segunda en $x = x_1$:

$$ f(x_2) \ge f(x_1) + f'(x_1)(x_2 - x_1) $$

$$ f(x_1) \ge f(x_2) + f'(x_2)(x_1 - x_2) $$

Gráficamente:

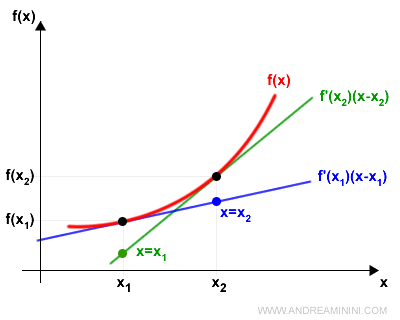
Sumando ambas desigualdades obtenemos:

$$ 0 \ge f'(x_1)(x_2 - x_1) + f'(x_2)(x_1 - x_2) $$

Reordenando términos:

$$ [f'(x_2) - f'(x_1)](x_2 - x_1) \ge 0 $$

Como $x_2 - x_1 > 0$, se deduce que:

$$ f'(x_2) - f'(x_1) \ge 0 \quad \forall x \in (x_1, x_2) $$

Es decir, $f'(x)$ es creciente en $[x_1, x_2]$. Por el criterio de monotonía, si $f'(x)$ es creciente, entonces $f''(x) \ge 0$ en $[x_1, x_2]$:

$$ f''(x) \ge 0 \quad \forall x \in (x_1, x_2) $$

Con esto queda demostrado que, si $f(x)$ es convexa, entonces $f'(x)$ es creciente y $f''(x) \ge 0$.

Demostración - Parte 2

Veamos ahora la recíproca: si $f'(x)$ es creciente, entonces $f(x)$ es convexa.

Tomemos dos puntos distintos $x$ y $x_0$ en $[a, b]$:

$$ x \ne x_0 $$

Por el Teorema del valor medio, existe un punto $x_1$ entre $x$ y $x_0$ tal que:

$$ f'(x_1) = \frac{f(x) - f(x_0)}{x - x_0} $$

o, de manera equivalente:

$$ f(x) - f(x_0) = f'(x_1)(x - x_0) $$

Dado que $f'(x)$ es creciente en $[a, b]$, distinguimos dos situaciones:

• Caso 1: $x < x_0$ En este caso, $(x - x_0) < 0$ y $x_1 \in (x, x_0)$, luego $x_1 < x_0$. Como $f'(x)$ es creciente: $$ f'(x_1) \le f'(x_0) $$ Al multiplicar por $(x - x_0)$ (negativo), la desigualdad se invierte: $$ f'(x_1)(x - x_0) \ge f'(x_0)(x - x_0) $$ Sustituyendo: $$ f(x) - f(x_0) \ge f'(x_0)(x - x_0) $$
• Caso 2: $x > x_0$ Aquí, $(x - x_0) > 0$ y $x_1 \in (x_0, x)$, por tanto $x_1 > x_0$. Como $f'(x)$ es creciente: $$ f'(x_1) \ge f'(x_0) $$ Al multiplicar por $(x - x_0) > 0$, la desigualdad se conserva: $$ f'(x_1)(x - x_0) \ge f'(x_0)(x - x_0) $$ Sustituyendo: $$ f(x) - f(x_0) \ge f'(x_0)(x - x_0) $$

En ambos casos se concluye que:

$$ f(x) \ge f(x_0) + f'(x_0)(x - x_0) $$

El segundo miembro no es más que la ecuación de la tangente en $x_0$.

Como la función queda por encima de su tangente, resulta convexa.

Q.E.D.