Funciones Numéricas
Una función se denomina función numérica cuando tanto su dominio como su codominio están formados por conjuntos numéricos.
La regla que determina la función se expresa mediante su expresión analítica.
Por ejemplo:
$$ y = f(x) = 2x+1 $$
La expresión analítica de la función f(x) es y = 2x + 1.
En este caso se trata de una función de una sola variable.
- La variable y recibe el nombre de variable dependiente, ya que su valor "depende" del valor de x.
- La variable x se denomina variable independiente, porque su valor "no depende" de ninguna otra variable.
El conjunto de todos los valores posibles que puede tomar la variable independiente (x) se llama dominio, dominio natural o dominio de definición de la función.
Por el contrario, el conjunto de valores que puede asumir la variable dependiente (y) se denomina codominio.
Un Ejemplo Práctico
Consideremos la función:
$$ y = \frac{x+1}{x} $$
El dominio de esta función está constituido por todos los números reales excepto el cero:
$$ D_f = \mathbb{R} \setminus \{ 0 \} $$
El cero queda excluido del dominio porque la función no está definida en x = 0: la división entre cero no es posible.
Por lo tanto, la variable independiente puede tomar cualquier valor real dentro de los intervalos (-∞, 0) ∪ (0, ∞).
Para representar gráficamente la función comenzamos construyendo un diagrama cartesiano.
El primer paso consiste en elaborar una tabla que relacione algunos valores de x con sus correspondientes valores de y. Cada fila de la tabla representa un par ordenado (x, y).
$$ \begin{array}{c|c} x & y \\ \hline -3 & 0.66 \\ -2 & 0.5 \\ -1 & 0 \\ -0.5 & -1 \\ 0 & \text{indefinido} \\ 0.5 & 3 \\ 1 & 2 \\ 2 & 1.5 \\ 3 & 1.33 \end{array} $$
A continuación, trazamos un diagrama cartesiano, colocando el dominio (x) sobre el eje horizontal y el codominio (y) sobre el eje vertical.
También establecemos la orientación y la unidad de medida en cada eje.
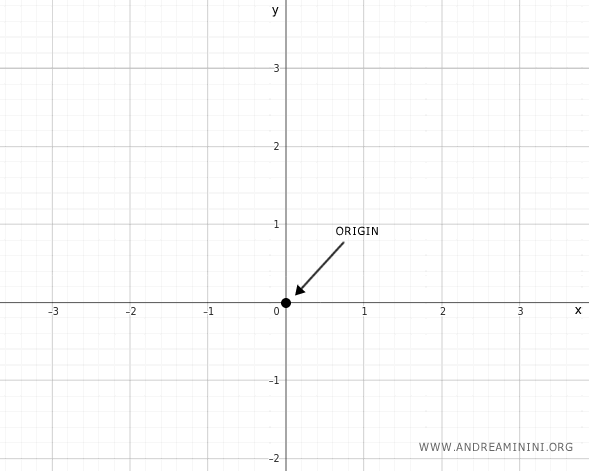
El punto donde se cruzan los dos ejes se llama origen O y corresponde al par ordenado (0, 0).
Luego situamos en el plano cartesiano los puntos que representan los pares ordenados (x, y) obtenidos en la tabla.
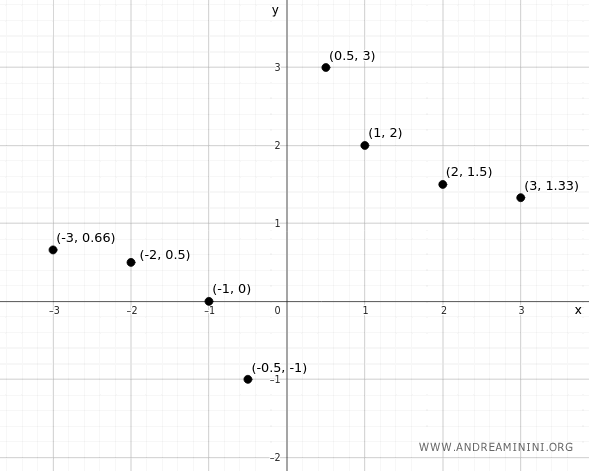
El conjunto de todos estos puntos constituye la gráfica de la función.
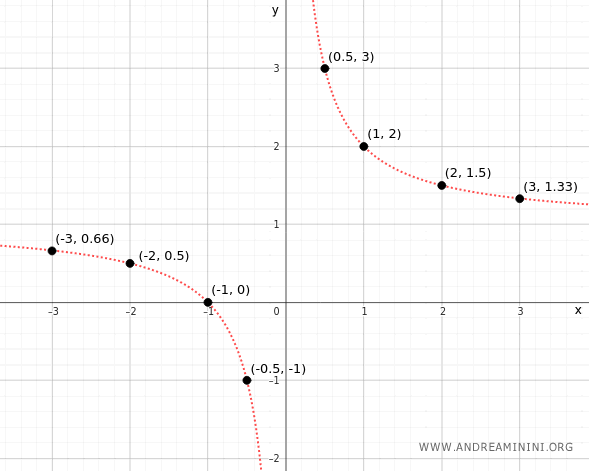
Y así se construye la representación gráfica de la función.