Funciones Inversamente Proporcionales
Una función se denomina inversamente proporcional cuando puede expresarse como $$ y = \frac{k}{x} $$, siendo k una constante real distinta de cero (k≠0).
Las variables x e y son inversamente proporcionales porque su producto se mantiene constante.
$$ y = \frac{k}{x} $$
Si multiplicamos ambos lados de la ecuación por x obtenemos:
$$ y \cdot x = \frac{k}{x} \cdot x $$
lo que se simplifica en un producto constante:
$$ y \cdot x = k $$
Dicho de otro modo, si una variable se duplica, la otra debe reducirse a la mitad para que el producto xy no varíe.
Esta propiedad se cumple para todos los valores de x salvo en cero, ya que la función no está definida en x=0 (división por cero).
$$ y = \frac{k}{x} $$
Nota. La gráfica de una función inversamente proporcional es una hipérbola rectangular. En cualquier punto de la curva, el rectángulo formado por sus proyecciones sobre los ejes conserva siempre la misma área.
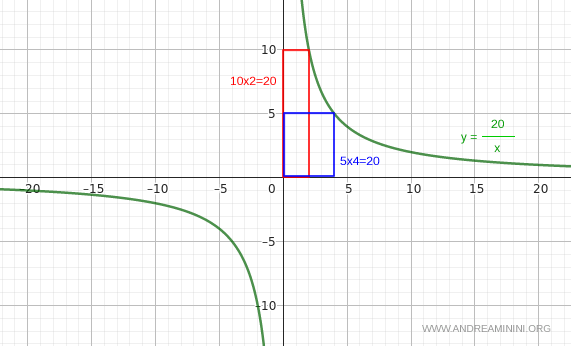
Un Ejemplo Ilustrativo
Consideremos la función:
$$ y = \frac{20}{x} $$
Queremos verificar si cumple la condición de proporcionalidad inversa.
Al construir una tabla de valores para x, y y su producto obtenemos:
$$ \begin{array}{c|c} x & y & x \cdot y \\ \hline -2 & -10 & 20 \\ -1 & -20 & 20 \\ 0 & \text{indef.} & \text{indef.} \\ 1 & 20 & 20 \\ 2 & 10 & 20 \\ 4 & 5 & 20 \end{array} $$
El producto se mantiene constante para cada par (x,y) con x≠0.

Por lo tanto, la función y=20/x es, en efecto, una función inversamente proporcional.
Y así sucesivamente...