Función logarítmica
La función logarítmica es aquella en la que la variable aparece dentro del argumento de un logaritmo: $$ y = \log_b x $$ donde $b$ es un número real positivo ($b>0$), distinto de $1$ ($b\neq1$), llamado base del logaritmo.
Para cualquier base $b>0$ con $b\neq1$, la función logarítmica solo está definida para valores positivos de $x$.
En consecuencia, su dominio es el conjunto de los números reales positivos $R^+$, mientras que su recorrido corresponde a todos los números reales $R$.
$$ f : R^+ \rightarrow R $$
En la figura siguiente se representa la gráfica del logaritmo en base 10 ($\log_{10}$) junto con el logaritmo natural ($\ln$), cuya base es el número de Euler $e$.
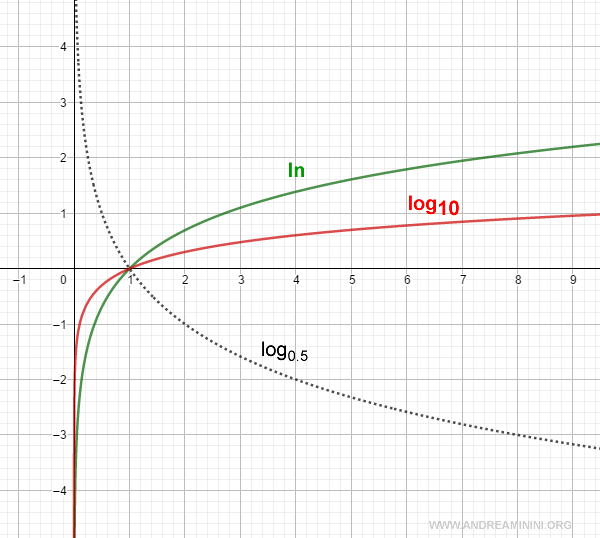
La gráfica de la función logarítmica pasa por el punto (1; 0), donde corta el eje \( x \), y no presenta intersección alguna con el eje \( y \).
Si la base es mayor que 1, la función logarítmica resulta creciente:
- Es negativa cuando $0 < x < 1$.
- Es positiva cuando $x > 1$.
Si la base está entre 0 y 1, la función logarítmica es decreciente:
- Toma valores negativos para $x > 1$.
- Toma valores positivos cuando $0 < x < 1$.
En ambos casos, la función logarítmica es biyectiva y, por lo tanto, tiene inversa.
La función inversa de un logaritmo es una función exponencial de la forma $b^y$, con $y = \log_b x$.
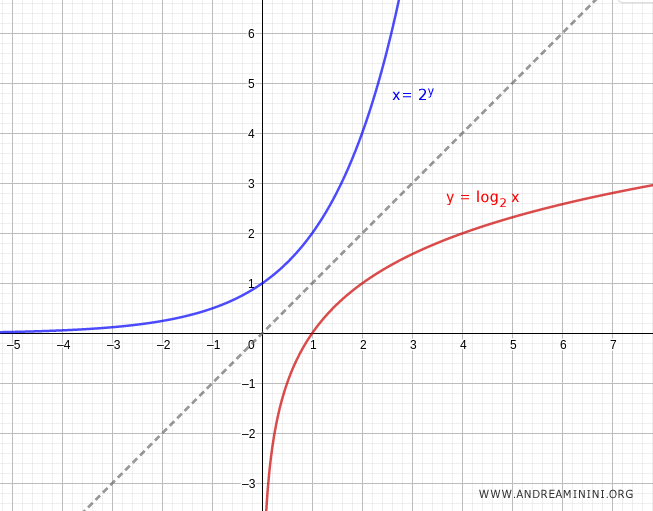
Ejemplo. La función logarítmica en base 2 es invertible. Su inversa corresponde a la función exponencial $2^y$.
Las gráficas de $b^y$ y $y = \log_b x$ son simétricas respecto de la recta $y = x$, la bisectriz de los cuadrantes primero y tercero.
Observaciones adicionales
Algunas propiedades importantes:
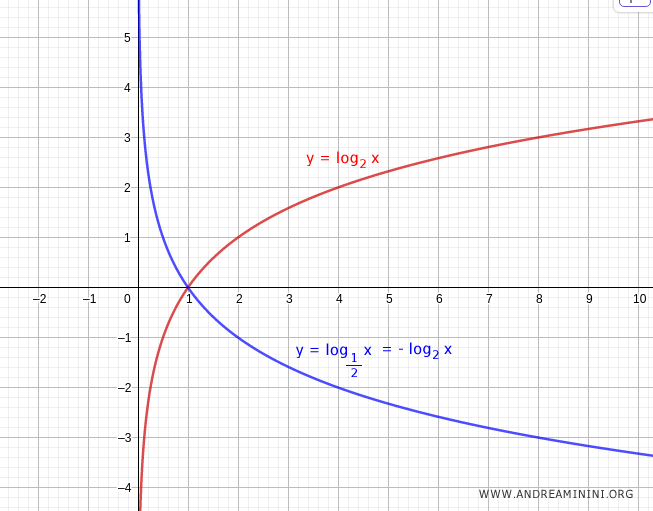
- El logaritmo en base recíproca equivale al opuesto del logaritmo en la base original: $$ \log_{\tfrac{1}{b}} x = - \log_b x $$
Demostración. Consideremos $\log_{\tfrac{1}{2}} x$. Aplicando la fórmula del cambio de base, $$ \log_{\tfrac{1}{2}} x = \frac{\log_2 x}{\log_2 \tfrac{1}{2}} .$$ Como $\log_2 \tfrac{1}{2} = -1$, se obtiene $$ \log_{\tfrac{1}{2}} x = \frac{\log_2 x}{-1} = -\log_2 x .$$ De esta manera queda establecida la relación entre el logaritmo en base $b$ y el de base $1/b$.
- Una función logarítmica simétrica respecto al eje $x$ puede obtenerse de dos formas: usando la base recíproca $1/b$ o simplemente tomando el opuesto $-\log_b x$ con la misma base.
Y así sucesivamente…