Función creciente

Una función y=f(x) se dice creciente en un intervalo I=(a,b) si, para cualesquiera dos puntos x₁, x₂ del intervalo con x₁<x₂, se cumple $$ f(x_1) \le f(x_2) $$. En cambio, se llama estrictamente creciente cuando se verifica que $$ f(x_1) < f(x_2) $$.

A veces, una función estrictamente creciente también se describe como “creciente en sentido estricto”.

Las funciones crecientes y estrictamente crecientes forman parte de la familia más amplia de las funciones monótonas.

Nota. Una función es monótona en un intervalo de su dominio cuando, en todo ese intervalo, se mantiene siempre creciente o siempre decreciente.

Ejemplo

Consideremos la función

$$ y=x^2 $$

Esta función es estrictamente creciente en el intervalo (1,5), ya que para cualesquiera dos valores x₁<x₂ comprendidos en ese rango se cumple f(x₁)<f(x₂).

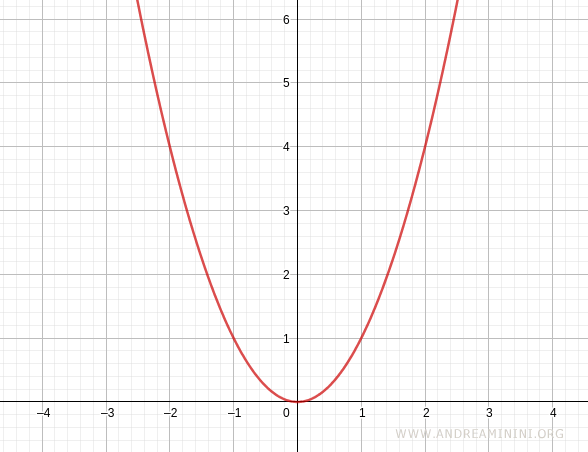
En cambio, la misma función no resulta creciente en el intervalo (-5,-1).

Nota. La monotonicidad de una función continua y derivable también puede estudiarse aplicando la prueba de la primera derivada.

Y así sucesivamente.