Función de valor absoluto

La función de valor absoluto (también llamada función módulo) es aquella en la que la variable aparece encerrada entre barras de valor absoluto: $$ f(x) = |x| $$

Esta función devuelve siempre un número no negativo, es decir, positivo o igual a cero.

Por ejemplo, el valor absoluto de -3 es 3:

$$ | -3 | = 3 $$

En otras palabras, la función elimina el signo negativo de la entrada y devuelve su correspondiente positivo.

El valor absoluto se denota escribiendo la variable entre dos barras verticales:

$$ f(x) = |x| $$

De manera equivalente, puede definirse como una función a trozos:

$$ y = |x| = \begin{cases} x & \text{si } x \geq 0 \\ \\ -x & \text{si } x < 0 \end{cases} $$

Es decir:

• y = x cuando x es mayor o igual que cero,
• y = -x cuando x es menor que cero.

En programación suele escribirse como abs(), abreviatura del término inglés absolute value:

$$ y = abs(x) $$

Otra forma de expresarlo es como la raíz cuadrada del cuadrado de la entrada: $$ y = |x| = \sqrt{x^2} $$

¿Por qué es útil? El valor absoluto tiene numerosas aplicaciones. Una de las más comunes es el cálculo de distancias entre dos puntos.

Ejemplo práctico

Veamos algunos casos sencillos:

El valor absoluto de -3 es 3:

$$ | -3 | = 3 $$

El valor absoluto de -4.2 es 4.2:

$$ | -4.2 | = 4.2 $$

El valor absoluto de 4 es 4:

$$ |4| = 4 $$

El valor absoluto de -121 es 121:

$$ |-121| = 121 $$

Nota. El único caso especial es el cero: como no tiene signo, su valor absoluto es simplemente cero. $$ |0| = 0 $$

La gráfica de la función valor absoluto

La gráfica de la función de valor absoluto nunca toma valores negativos, por lo que se sitúa completamente por encima (o sobre) el eje x.

El ejemplo clásico es f(x)=|x|, cuya representación en el plano cartesiano es la siguiente:

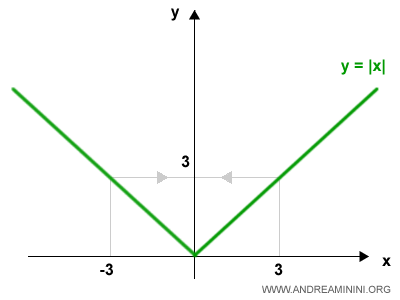
La función f(x)=|x| está formada por dos semirrectas: y = x para x > 0 e y = -x para x < 0, que se encuentran en el origen.

En el punto (0,0) la gráfica presenta un vértice. Esto implica que la función es continua en ese punto, pero no es derivable allí.

Nota. El argumento dentro del valor absoluto puede ser cualquier expresión. Por ejemplo, f(x)=|2x| o f(x)=|x²+1|. En tales casos, la gráfica puede adoptar formas distintas, como una parábola, según la expresión considerada. Por ejemplo, la gráfica de f(x)=|x³| recuerda a una parábola.

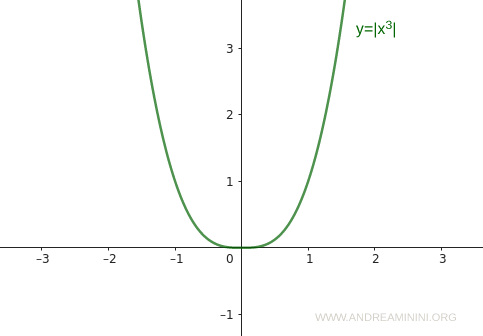
En cualquier caso, la gráfica permanece siempre sobre o en el eje x.

Y así sucesivamente.