Función periódica
Qué son las funciones periódicas
Se dice que una función $ y=f(x) $ es periódica de período $ T $, con $ T>0 $, cuando se cumple la condición $$ f(x+kT)=f(x) $$ para todo $ x $ del dominio y para todo entero $ k $.
En términos gráficos, una función periódica presenta un comportamiento que se repite de manera regular. La forma de la gráfica se reproduce una y otra vez a intervalos constantes iguales al período.
De este modo, si una función es periódica de período T, también lo será con cualquier período que sea un múltiplo entero de T.
$$ f(x+T) = f(x+kT) = f(x) $$
Esto sucede porque los valores $ x $, $ x+T $ y $ x+kT $ se corresponden con un mismo valor de la función.
Por ejemplo, si una función es periódica de período T, entonces también es periódica con período 2T, 3T, 4T, y así sucesivamente. El menor período positivo T recibe el nombre de período fundamental.
Un ejemplo práctico
Un caso clásico es la función coseno, que es una función periódica cuyo período es T=2π.
$$ y = \cos(x) $$
Por ejemplo, cuando x=0 y x=2π, la función f(x) toma exactamente el mismo valor.
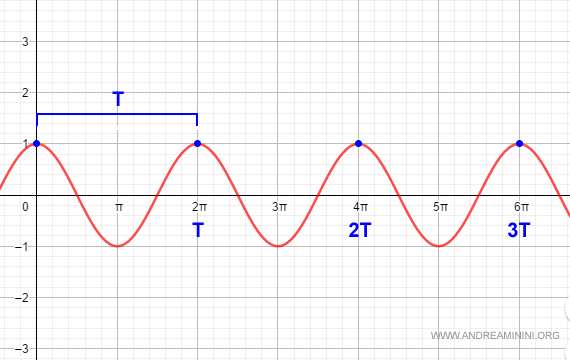
Ese mismo valor vuelve a aparecer para x=4π. El mismo patrón se repite para x=6π, y continúa de la misma forma para todos los múltiplos enteros de 2π.
$$ \cos(0) = \cos(2 \pi ) = \cos (4 \pi ) $$
De manera más general, la función $ f=\cos(x) $ reproduce los mismos valores de su imagen para cada múltiplo entero del período T.
$$ \cos (x) = \cos(x+kT) $$
Por lo tanto, la función coseno es periódica con $ T=2 \pi $.
Notas
Algunas observaciones adicionales que ayudan a comprender mejor las funciones periódicas:
- Una función periódica no es inyectiva
En una función periódica existe un período \( T \neq 0 \) tal que \( f(x+T)=f(x) \) para todo \( x \) del dominio. Como consecuencia, un mismo valor del codominio es alcanzado por infinitos elementos distintos del dominio, separados entre sí por múltiplos enteros de \( T \). Por esta razón, una función periódica no puede ser inyectiva. A la inversa, si una función es inyectiva, entonces no puede ser periódica.
Y así sucesivamente.