Función identidad

La función identidad aparece cuando una función f:A→B se compone con su función inversa f^-1:B→A. $$ f^{-1} \circ f(x) = x $$ En otras palabras: $$ f^{-1}[f(x)] = x $$

Se denomina función identidad porque asigna a cada elemento x de su dominio a sí mismo:

$$ f^{-1}[f(x)] = x $$

La composición inversa también se verifica:

$$ f[f^{-1}(y)] = y $$

A continuación se muestra una representación de la función identidad mediante diagramas de Euler-Venn:

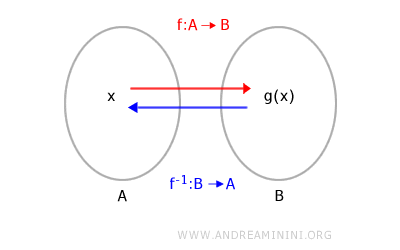
La función identidad se considera *simple* cuando se aplica a un conjunto, en cuyo caso corresponde a una biyección.

Observación. La función identidad es compatible con todas las estructuras matemáticas (por ejemplo, espacios vectoriales, estructuras algebraicas, espacios métricos, espacios topológicos, etc.). Según el contexto, adopta interpretaciones específicas: en una estructura algebraica actúa como un isomorfismo; en un espacio vectorial, como una aplicación lineal; en un espacio métrico, como una isometría; y en un espacio topológico, como un homeomorfismo.

Un ejemplo práctico

Consideremos la función f(x) = x²:

$$ y = x^2 $$

y su inversa: $$ x = \sqrt{y} $$

La composición de ambas funciones resulta:

$$ f^{-1}[f(x)] = \sqrt{x^2} = x $$

Se trata de una función identidad porque cada elemento x se corresponde consigo mismo.

Observación. También se cumple la composición inversa: $$ f[f^{-1}(x)] = (\sqrt{x})^2 = x $$

Ejemplo 2

Consideremos ahora la función f(x) = 2x:

$$ y = 2x $$

y su inversa: $$ x = \frac{y}{2} $$

Su composición es:

$$ f^{-1}[f(x)] = \frac{2x}{2} = x $$

Observación. También en este caso se verifica la composición inversa: $$ f[f^{-1}(x)] = 2 \left( \frac{x}{2} \right) = x $$

Ejemplo 3

Finalmente, consideremos la función f(x) = sen(x):

$$ y = \sin(x) $$

y su inversa: $$ x = \arcsin(y) $$

Su composición resulta:

$$ f^{-1}[f(x)] = \arcsin[\sin(x)] = x $$

Observación. También aquí se cumple la composición inversa: $$ f[f^{-1}(x)] = \sin(\arcsin x) = x $$

Y así sucesivamente.