La derivada del arcoseno
La derivada de la función arcoseno es: $$ D[\arcsin x] = \frac{1}{\sqrt{1 - x^2}}. $$
Este resultado se deduce del hecho de que la función arcoseno es la inversa de la función seno.
Nota. En trigonometría, la función arcoseno (arcsin) se define como la inversa de la función seno en el intervalo [-π/2, π/2].
Cómo entender la función arcoseno
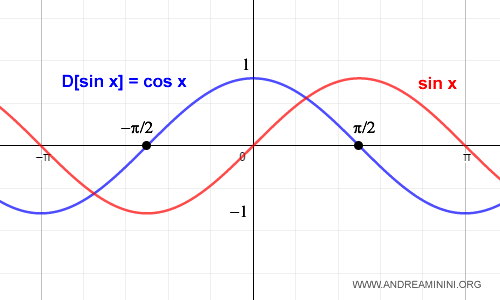
La función seno no es monótona en todo su dominio de números reales.
Sin embargo, se convierte en una función continua y estrictamente monótona cuando se restringe al intervalo [-π/2, π/2].
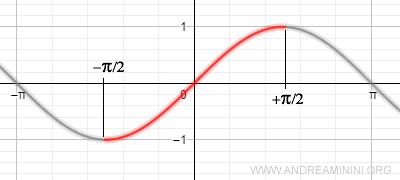
En ese intervalo, el seno toma todos los valores comprendidos entre su mínimo -1 y su máximo 1.
Al ser continua y monótona en [-π/2, π/2], la función seno resulta invertible en dicho rango.
La función inversa del seno se denomina función arcoseno:
$$ f^{-1}(x) = \arcsin x $$
¿Por qué se llama arcoseno? Se llama así porque representa el arco de longitud $x$ en la circunferencia unitaria; en otras palabras, el ángulo (en radianes) cuyo seno es igual a un valor dado.
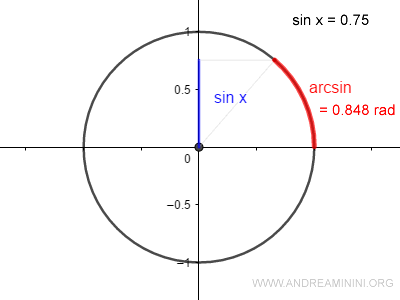
Como seno y arcoseno son funciones inversas: $$ y = \sin x \\ x = \arcsin y $$ Por lo tanto: $$ y = \sin(\arcsin y) \\ x = \arcsin(\sin x) $$
El dominio de la variable independiente de la función arcoseno es el intervalo cerrado [-1, 1].
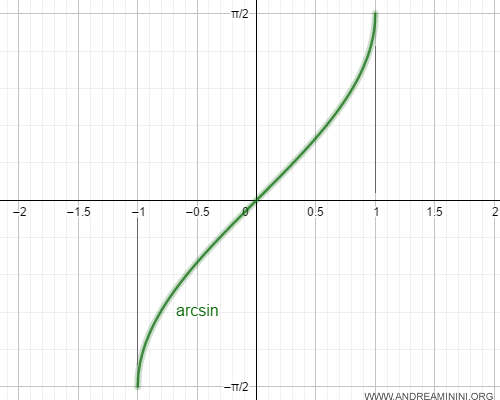
En consecuencia, la función arcoseno es derivable en el intervalo abierto (-1, 1).
Demostración y explicación
La función arcoseno es la inversa de la función seno.
$$ f^{-1}(f(y)) = \arcsin x $$
donde $f(y)$ está definida como:
$$ f(y) = \sin y $$
De ahí que podamos aplicar la regla de la derivada de la función inversa:
$$ D[f^{-1}] = \frac{1}{D[f(y)]}. $$
Así, para la función arcoseno:
$$ D[\arcsin x] = \frac{1}{D[\sin y]}. $$
Como la derivada del seno es el coseno, se obtiene:
$$ D[\arcsin x] = \frac{1}{\cos y}. $$
Nota. Recuerda la identidad trigonométrica: $$ \cos y = \sqrt{1 - \sin^2 y}. $$
Por lo tanto:
$$ D[\arcsin x] = \frac{1}{\sqrt{1 - \sin^2 y}}. $$
Nota. Como $$ y = \arcsin x, $$ se sigue que $$ \sin y = \sin(\arcsin x) = x. $$ De este modo, podemos sustituir y expresar la derivada únicamente en función de $x$: $$ \sin^2 y = \sin^2(\arcsin x) = x^2. $$
Así obtenemos finalmente:
$$ D[\arcsin x] = \frac{1}{\sqrt{1 - x^2}}. $$
Con esto queda demostrada la fórmula de la derivada de la función arcoseno.
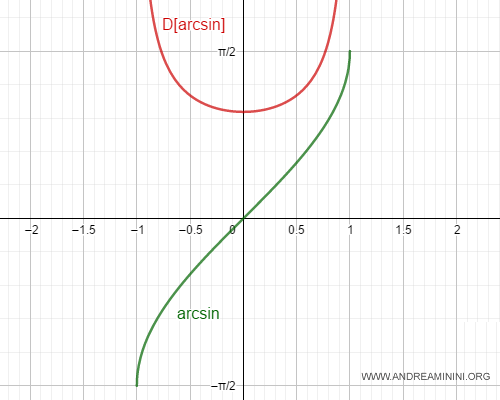
Nota. La función arcoseno no es derivable en $x = 1$ ni en $x = -1$, pues $\arcsin(1) = \pi/2$ y $\arcsin(-1) = -\pi/2$. En estos puntos, el seno vale $\pm 1$: $$ \sin(\pi/2) = 1 \\ \sin(-\pi/2) = -1 $$ La derivada del seno es el coseno, y en esos valores el coseno es cero: $$ \cos(\pi/2) = 0 \\ \cos(-\pi/2) = 0 $$
En consecuencia, la derivada de la función arcoseno no está definida en $x = \pm 1$, lo que genera una asíntota vertical en dichos puntos.
Y así continúa.