Teorema de Fermat

Si una función $ f(x) $ definida en el intervalo [a, b] alcanza un máximo o un mínimo local en un punto $ x₀ $, entonces su primera derivada en ese punto debe anularse: $$ f'(x_0)=0 $$

Existe un mínimo local si, en un entorno de $ x₀ $, la derivada lateral izquierda es negativa y la derecha positiva: $$ f'_-(x_0) < 0 \:\:\:, \:\:\: f'_+(x_0) > 0 $$
Existe un máximo local si, cerca de $ x₀ $, la derivada lateral izquierda es positiva y la derecha negativa: $$ f'_-(x_0) > 0 \:\:\:, \:\:\: f'_+(x_0) < 0 $$

Nota. El teorema de Fermat tiene una restricción: solo se aplica cuando $ x₀ $ es un punto interior del intervalo [a, b]. En los extremos a o b no puede emplearse, ya que allí no existen derivadas por ambos lados.

Un ejemplo práctico
Demostración
Extremos en los extremos del intervalo

Un ejemplo práctico

Consideremos la función $ f(x) $ definida en los números reales:

$$ f(x)=x^2 $$

Su primera derivada es:

$$ f'(x)=2x $$

La derivada se anula únicamente en $ x=0 $:

$$ f'(0)=0 $$

Por tanto, en $ x=0 $ la función puede presentar un máximo o un mínimo local.

¿Se trata de un mínimo o de un máximo?

Para resolverlo, estudiamos las derivadas laterales en torno a $ x₀=0 $:

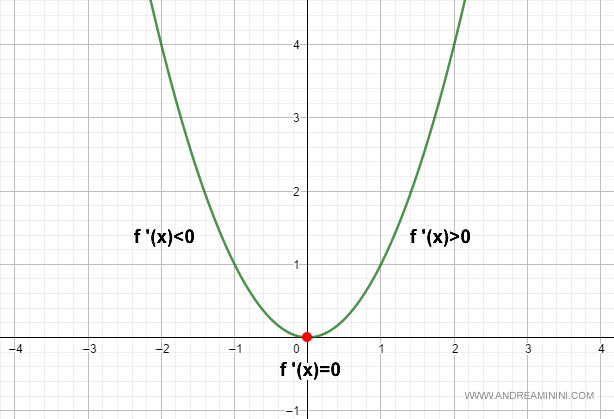
$$ f'_-(0) < 0 $$

$$ f'_+(0) > 0 $$

Como la función decrece a la izquierda (derivada negativa) y crece a la derecha (derivada positiva), el punto $ x₀=0 $ es un mínimo local.

Ilustración del teorema de Fermat

Nota. Si la función es dos veces derivable, también puede determinarse el tipo de extremo analizando el signo de la segunda derivada. Si $ f''(x_0) \ge 0 $, el punto es un mínimo; si $ f''(x_0) \le 0 $, es un máximo.

Demostración

Supongamos que una función definida en [a, b] alcanza un máximo local en $ x₀ $. En tal caso, debe crecer a la izquierda de $ x₀ $ y decrecer a la derecha.

Esto se traduce en que la derivada primera resulta positiva a la izquierda y negativa a la derecha de $ x₀ $:

$$ f'_-(x_0) = \lim_{h \rightarrow 0^-} \frac{f(x_0+h)-f(x_0)}{h} \ge 0 $$

$$ f'_+(x_0) = \lim_{h \rightarrow 0^+} \frac{f(x_0+h)-f(x_0)}{h} \le 0 $$

Según los criterios de derivabilidad en un punto, una función es derivable en $ x₀ $ cuando ambas derivadas laterales existen, son iguales y coinciden con $ f'(x_0) $.

Por ello, la derivada en $ x₀ $ debe ser cero, único valor que satisface ambas condiciones:

$$ f'(x_0) = \lim_{h \rightarrow 0} \frac{f(x_0+h)-f(x_0)}{h} = 0 $$

Nota. El razonamiento para un mínimo local es análogo: en ese caso la función decrece a la izquierda (derivada negativa) y crece a la derecha (derivada positiva). Si la función es derivable en $ x₀ $, la derivada debe anularse para coincidir con los valores de ambas derivadas laterales.

Extremos en los extremos del intervalo

Para determinar si un extremo de un intervalo corresponde a un máximo o a un mínimo local, se estudia la derivada lateral y el comportamiento de la función en sus cercanías. Un extremo es un máximo si: $$ f'(x_0) \cdot (x - x_0) \le 0 $$ Es un mínimo si: $$ f'(x_0) \cdot (x - x_0) \ge 0 $$

Ejemplo

Consideremos la función $ f(x)=2x $ definida en el intervalo [5, 10]:

Queremos verificar si el extremo derecho $ x=10 $ (punto B) es un máximo local.

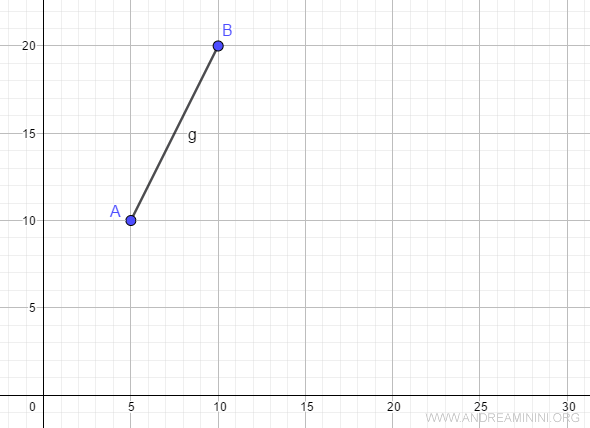
Gráfico con extremos en los límites del intervalo

En $ x=10 $ no existe derivada lateral derecha, pues se trata del extremo del intervalo.

En cambio, la derivada lateral izquierda sí existe y es:

$$ f'_-(10)=2 $$

Aplicamos la condición para estudiar el comportamiento de la función en el intervalo:

$$ f'(x_0) \cdot (x - x_0) $$

$$ 2 \cdot (x - 10) $$

Obsérvese que, para cualquier $ x \in [5, 10] $, esta expresión es siempre menor o igual que cero, ya que $ (x - 10) $ resulta negativo (o nulo en $ x=10 $):

$$ 2 \cdot (x - 10) \le 0 $$

Por lo tanto, el punto $ x=10 $ constituye un máximo local.

Nota. El mismo criterio sirve para verificar si el extremo B es un mínimo local. Además, el método también puede aplicarse a puntos interiores. Por ejemplo, consideremos la función $ f(x)=\sin x $ definida en el intervalo [1, 2]. Su derivada es $ f'(x)=\cos x $. Queremos determinar si el punto $ x=\pi/2 $ corresponde a un mínimo, un máximo o ninguno de los dos.
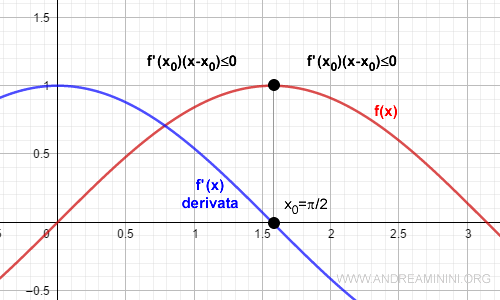
Ejemplo con un punto interior del intervalo
Analicemos el entorno de $ x=\pi/2 $. A la izquierda, la derivada lateral $ f'_-(x₀)>0 $ y $ (x - x₀)<0 $. A la derecha, la derivada lateral $ f'₊(x₀)<0 $ y $ (x - x₀)>0 $. En ambos casos, alrededor de $ x₀=\pi/2 $, la expresión resulta siempre menor o igual que cero: $$ f'(x_0) \cdot (x - x_0) \le 0 $$ De este modo, $ x=\pi/2 $ es un punto de máximo local para la función $ f(x)=\sin x $.

Y así sucesivamente.