Derivada de la función coseno
Definición
La derivada de la función coseno es: $$ D[\cos x] = -\sin x $$
Demostración
Vamos a obtener este resultado evaluando el cociente incremental de la función coseno:
$$ \lim_{h \rightarrow 0} \frac{\cos(x+h) - \cos(x)}{h} $$
Para ello utilizamos la siguiente identidad trigonométrica:
$$ \cos a - \cos b = -2 \sin \left(\frac{a - b}{2}\right) \cdot \sin \left(\frac{a + b}{2}\right) $$
Aplicando esta identidad al numerador, tenemos:
$$ a = x + h $$
$$ b = x $$
De este modo, el cociente incremental queda transformado en:
$$ \lim_{h \rightarrow 0} \frac{-2 \cdot \sin \left(\frac{h}{2}\right) \cdot \sin \left(x + \frac{h}{2}\right)}{h} $$
Multiplicando numerador y denominador por \( \frac{1}{2} \), la expresión se simplifica a:
$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right) \cdot \sin \left(x + \frac{h}{2}\right)}{\frac{h}{2}} $$
Este límite puede descomponerse en dos factores:
$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} \cdot \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) $$
Analicemos ahora cada límite por separado.
El primero corresponde a un límite notable del cálculo diferencial:
$$ \lim_{t \rightarrow 0} \frac{\sin t}{t} = 1 $$
Sustituyendo \( t = \frac{h}{2} \), resulta:
$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} = -1 $$
El segundo límite se resuelve de forma inmediata:
$$ \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) = \sin x $$
Combinando ambos resultados se obtiene:
$$ \lim_{h \rightarrow 0} \frac{-\sin \left(\frac{h}{2}\right)}{\frac{h}{2}} \cdot \lim_{h \rightarrow 0} \sin \left(x + \frac{h}{2}\right) = -1 \cdot \sin x $$
Por lo tanto, la derivada de \(\cos x\) es:
$$ f'(x) = -\sin x $$
Hemos demostrado así que la derivada de la función coseno es, en efecto, \(-\sin x\).
Representación gráfica
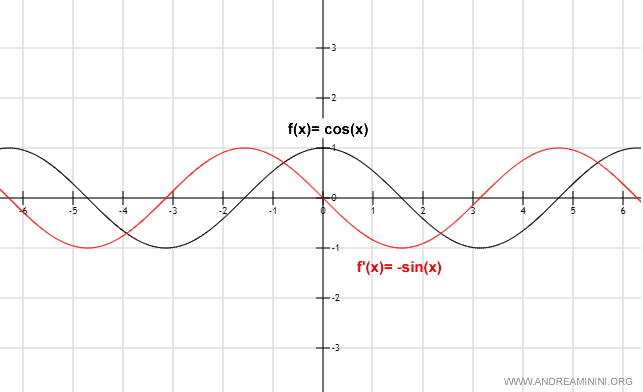
Un ejemplo práctico
Consideremos la siguiente función:
$$ f(x) = \cos (x^2) $$
Nota: Cuando el argumento de la función coseno no es simplemente \( x \), estamos ante una función compuesta de la forma \( f(g(x)) \). En este caso, la derivada no es simplemente \(-\sin(x^2)\); es necesario aplicar la regla de la cadena.
Al tratarse de una función compuesta, aplicamos la regla de la cadena:
$$ f'(x) = f'(g(x)) \cdot g'(x) $$
En nuestro caso:
$$ f'(g(x)) = D[\cos(g(x))] = -\sin(x^2) $$
$$ g'(x) = D[x^2] = 2x $$
Sustituyendo en la regla de la cadena, resulta:
$$ f'(x) = -\sin(x^2) \cdot 2x $$
En conclusión, la derivada de \(\cos(x^2)\) es:
$$ f'(x) = -2x \cdot \sin(x^2) $$
Representación gráfica
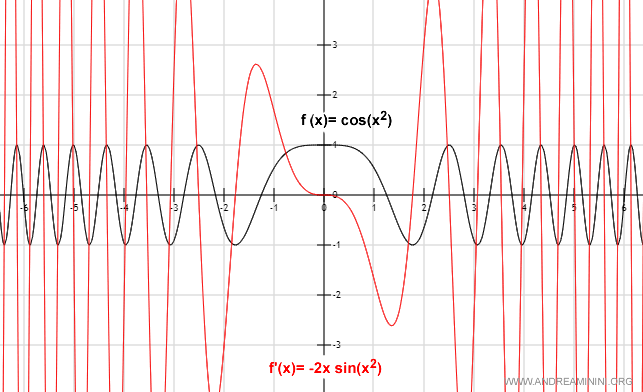
Y así sucesivamente.