Teorema de Lagrange
Enunciado del teorema de Lagrange
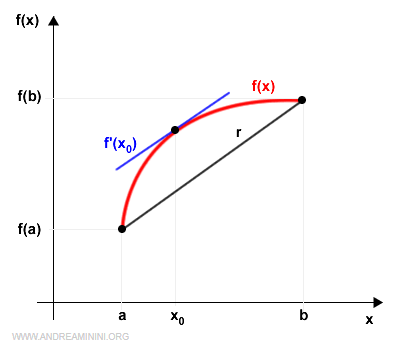
Sea \( f(x) \) una función continua en el intervalo [a,b] y derivable en (a,b). Entonces, existe al menos un punto \( x_0 \in (a,b) \) tal que la derivada en ese punto coincide con la pendiente de la recta secante que une los extremos del intervalo: $$ f'(x_0)=\frac{f(b)-f(a)}{b-a} $$
El teorema de Lagrange también se conoce como el teorema del valor medio del cálculo diferencial.
Ejemplo práctico
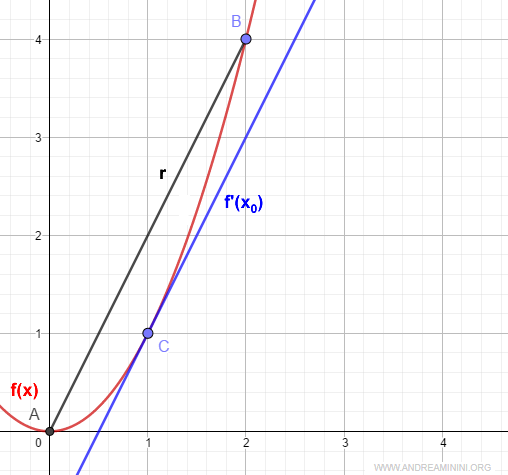
Consideremos la función \( f(x) = x^2 \), que es continua en el intervalo [0,2] y derivable en (0,2).
$$ f(x)=x^2 $$
El punto donde se cumple el teorema de Lagrange debe satisfacer:
$$ f'(x_0) = \frac{f(b)-f(a)}{b-a} $$
Como la derivada de \( f(x)=x^2 \) es \( f'(x)=2x \), resulta:
$$ 2x_0 = \frac{f(b)-f(a)}{b-a} $$
Con los extremos \( a=0 \) y \( b=2 \), se obtiene:
$$ 2x_0 = \frac{f(2)-f(0)}{2-0} $$
$$ 2x_0 = \frac{4-0}{2-0} $$
$$ 2x_0 = 2 $$
De donde se deduce:
$$ x_0 = \frac{2}{2} = 1 $$
En \( x_0 = 1 \), la derivada \( f'(x_0) \) coincide con la pendiente de la recta secante que une los extremos del intervalo [a,b].
Demostración y explicación
Sea \( f(x) \) una función continua en [a,b] y derivable en (a,b).
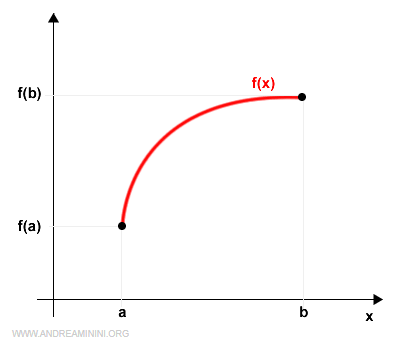
La ecuación de la recta secante que une los puntos extremos a y b es:
$$ r: f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) $$
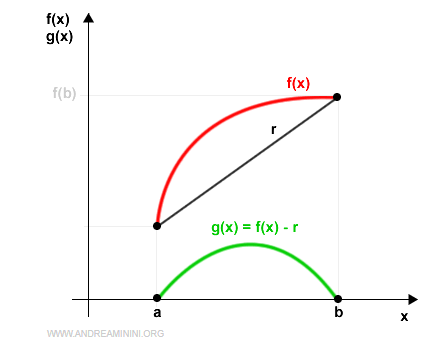
Representada en el plano cartesiano, se ve así:
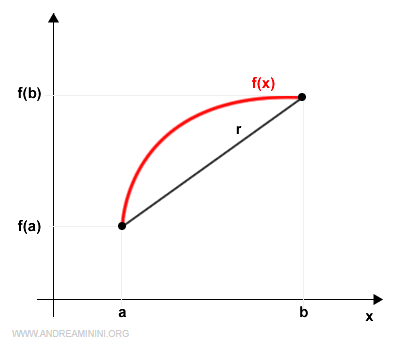
Definimos una nueva función \( g(x) \), que representa la diferencia entre f(x) y la recta r:
$$ g(x) = f(x) - r $$
$$ g(x) = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$
Por construcción, esta diferencia \( f(x) - r \) es igual a cero en los extremos a y b.
En consecuencia, g(x) también se anula en dichos puntos.
Verificación. En \( x = a \): $$ g(x) = f(x) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$ $$ g(a) = f(a) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (a - a) \right] $$ $$ g(a) = f(a) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot 0 \right] $$ $$ g(a) = f(a) - f(a) $$ $$ g(a) = 0 $$
En \( x = b \): $$ g(b) = f(b) - \left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (b - a) \right] $$ $$ g(b) = f(b) - \left[ f(a) + f(b) - f(a) \right] $$ $$ g(b) = f(b) - f(b) $$ $$ g(b) = 0 $$
Como g(x) se anula en los dos extremos, $$ g(a) = g(b) = 0 $$ por el teorema de Rolle, debe existir al menos un punto \( x_0 \in (a,b) \) en el que la derivada se anule: $$ g'(x_0)=0 $$
Derivamos g(x) en el intervalo (a,b):
$$ D[g(x)] = D\left[ f(x) - \left( f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right) \right] $$
$$ g'(x) = D[f(x)] - D\left[ f(a) + \frac{f(b)-f(a)}{b-a} \cdot (x - a) \right] $$
$$ g'(x) = f'(x) - \frac{f(b)-f(a)}{b-a} $$
Como \( g'(x_0) = 0 \), obtenemos:
$$ 0 = f'(x_0) - \frac{f(b)-f(a)}{b-a} $$
De aquí se concluye que la derivada es igual a la pendiente de la secante que une a y b:
$$ f'(x_0) = \frac{f(b)-f(a)}{b-a} $$
Desde un punto de vista geométrico, la tangente en \( x_0 \) -es decir, la derivada \( f'(x_0) \)- tiene la misma pendiente que la recta secante r.

De este modo queda demostrada la validez del teorema de Lagrange.
Y así sucesivamente.