Diferenciabilidad de una función en un punto

Una función es diferenciable en un punto \( c \) cuando existen los límites laterales del cociente incremental y ambos coinciden. $$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} \\ \\ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

El límite lateral izquierdo del cociente incremental se denomina derivada lateral izquierda:

$$ f'(x) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} $$

De forma análoga, el límite lateral derecho recibe el nombre de derivada lateral derecha:

$$ f'(x) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

Se presentan dos casos posibles:

• Si ambos límites existen y son iguales, la función es diferenciable en \( c \).
• Si los límites no coinciden, la función no es diferenciable en \( c \).

Los puntos donde \( f(x) \) no resulta diferenciable se llaman puntos singulares.

Un ejemplo práctico

Consideremos la función valor absoluto:

$$ f(x) = |x| $$

Queremos verificar si es diferenciable en \( x = 0 \). Empecemos con el límite lateral derecho:

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{f(x + Δx) - f(x)}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|x + Δx| - |x|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|0 + Δx - 0|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$

Dado que \( Δx \) tiende a cero por la derecha, siempre es positivo, y el límite resulta igual a +1.

Calculemos ahora el límite lateral izquierdo en \( x = 0 \):

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{f(x + Δx) - f(x)}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|x + Δx| - |x|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|0 + Δx - 0|}{Δx} $$

$$ f'(0) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$

En este caso, como \( Δx \) se aproxima a cero por la izquierda, es negativo, y el límite toma el valor -1.

Conclusión

Los límites laterales del cociente incremental en \( x = 0 \) no son iguales:

$$ f'(0^+) = \lim_{Δx \rightarrow 0^+} \frac{|Δx|}{Δx} = +1 $$

$$ f'(0^-) = \lim_{Δx \rightarrow 0^-} \frac{|Δx|}{Δx} = -1 $$

Por lo tanto, aunque la gráfica de la función se une en un único punto, en \( x = 0 \) la función \( f(x) = |x| \) no es diferenciable, ya que los límites laterales difieren (+1 ≠ -1).

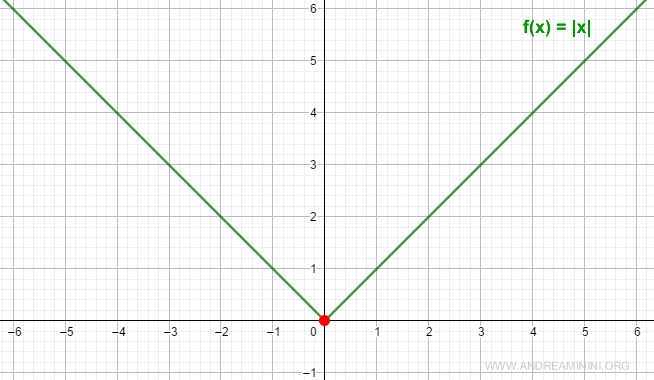
Nota. Este ejemplo muestra que la continuidad de una función en un punto es condición necesaria para que sea diferenciable, pero no suficiente. La función \( |x| \) es continua en \( x = 0 \), sin embargo no es diferenciable en ese punto.

Y así sucesivamente.