Cociente incremental de una función

Definición del cociente incremental

El cociente incremental de una función se define como: $$ \frac{f(x + h) - f(x)}{h} $$

El valor $h$ representa el incremento aplicado a la variable independiente.

Explicación

Consideremos una función $f(x)$ definida en un intervalo $(a, b)$:

$$ f(x) $$

Para comprender mejor el concepto, representemos la función $f(x)$ en el plano cartesiano:

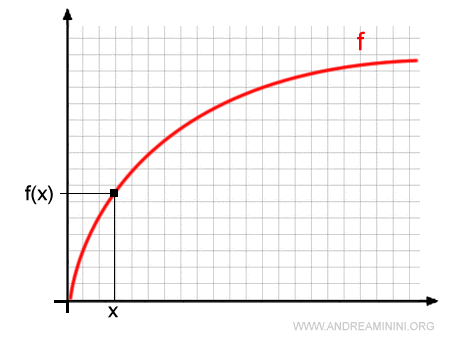
Escogemos ahora un valor arbitrario $h$ dentro del intervalo $(a, b)$, que actúa como incremento de la variable independiente $x$.

Al añadir este incremento, la función $f(x)$ adopta un nuevo valor:

$$ f(x + h) $$

Podemos visualizar esta variación en el plano cartesiano:

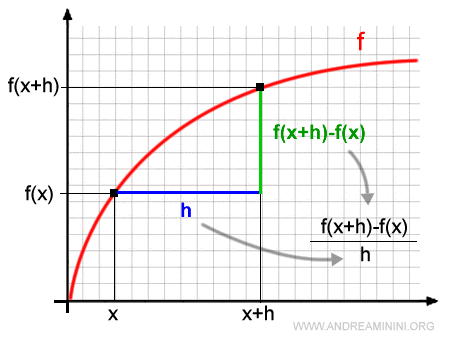
El cambio en la variable dependiente - es decir, la diferencia entre los valores de la función - se expresa como:

$$ f(x + h) - f(x) $$

La razón entre la variación de la variable dependiente y la del argumento se denomina cociente incremental:

$$ \frac{f(x + h) - f(x)}{h} $$

Nota. El cociente incremental de la función $f(x)$ está definido para todo $h$ perteneciente al intervalo $(a, b)$, salvo cuando $h = 0$. En ese caso, el denominador se anula y la fracción carece de sentido, ya que se produciría una división por cero.