Criterio de Monotonía Estricta

Función estrictamente creciente

Una función continua en [a,b] y derivable en (a,b) es estrictamente creciente en [a,b] si su primera derivada f'(x) cumple que f'(x) ≥ 0 para todo x ∈ [a,b], y no permanece igual a cero en ningún subintervalo de [a,b]. $$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

Función estrictamente decreciente

Una función continua en [a,b] y derivable en (a,b) es estrictamente decreciente en [a,b] si su primera derivada f'(x) cumple que f'(x) ≤ 0 para todo x ∈ [a,b], y no permanece igual a cero en ningún subintervalo de [a,b]. $$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \le 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

¿Puede la derivada de una función estrictamente creciente o decreciente anularse?

La derivada de una función estrictamente creciente o decreciente puede anularse en un punto aislado (por ejemplo, f'(x₀) = 0), pero no puede permanecer igual a cero en todo un intervalo de puntos.

Un ejemplo práctico

Ejemplo 1

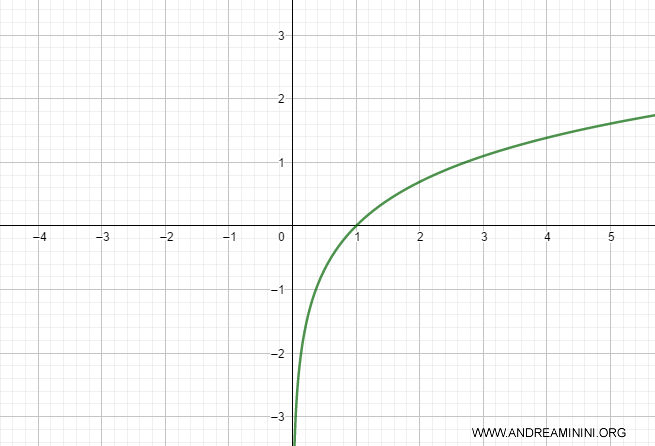
La función f(x) = log x es estrictamente creciente en el intervalo [0, ∞) porque su derivada f'(x) es ≥ 0 y no permanece en cero en ningún subintervalo.

Ejemplo 2

La función f(x) = x³ es estrictamente creciente en el intervalo [0, ∞) porque su derivada f'(x) es ≥ 0 y no se mantiene en cero en ningún subintervalo.

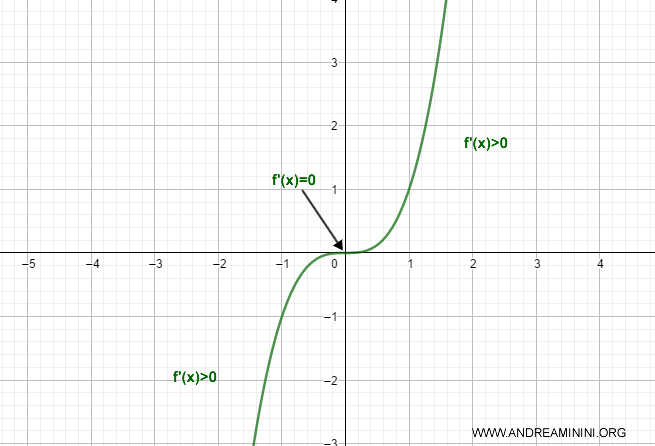
Nota. En el punto x = 0, la primera derivada de la función es cero, f'(x) = 0. Sin embargo, la función sigue siendo estrictamente creciente, ya que esto no contradice el criterio de monotonía estricta. Dicho criterio establece que la derivada no puede ser idénticamente cero en un intervalo.

Demostración

1] Comencemos con una función f(x) tal que f'(x) ≥ 0 para todo x ∈ [a,b] y f'(x) ≠ 0 en cualquier intervalo. Queremos demostrar que la función es estrictamente creciente.

$$ \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} \Rightarrow \text{estrictamente creciente} $$

Si la función no fuera estrictamente creciente, existirían dos puntos x₁ < x₂ tales que:

$$ f(x_1)=f(x_2) $$

En el intervalo (x₁, x₂) la función sería entonces constante, de acuerdo con el criterio de monotonía.

Pero esto contradice una de las hipótesis iniciales:

$$ \forall x \in [x_1, x_2] \:\: | \:\: f'(x) = 0 $$

Por lo tanto, las condiciones iniciales implican necesariamente que la función es estrictamente creciente.

Nota. Los puntos x₁ y x₂ no tienen por qué ser consecutivos. Como se supone que f(x) es creciente, si toma el mismo valor en ambos extremos, debe permanecer constante en todo el intervalo (x₁, x₂). No puede tomar valores mayores o menores dentro del intervalo sin violar la condición de ser creciente en (a,b).

2] Ahora, suponiendo que la función es estrictamente creciente, debemos demostrar que su derivada cumple que f'(x) ≥ 0 para todo x ∈ [a,b], y que f'(x) no es cero en ningún intervalo (x₁, x₂) ⊂ [a,b].

$$ \text{estrictamente creciente} \Rightarrow \begin{cases} \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 \\ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 \end{cases} $$

Si la derivada fuera negativa en algún punto, es decir, si f'(x) < 0 en algún x ∈ [a,b], la función dejaría de ser creciente y, por tanto, no podría ser estrictamente creciente.

De ello se deduce que la derivada debe ser no negativa en todo el intervalo:

$$ \forall x \in [a,b] \:\: | \:\: f'(x) \ge 0 $$

Si la derivada fuera nula en todo un intervalo [x₁, x₂], entonces la función sería constante en dicho intervalo, lo cual contradice la condición de monotonía estricta.

Por consiguiente, la derivada debe ser distinta de cero en cualquier intervalo:

$$ \forall (x_1,x_2) \subset (a,b) \:\: | \:\: f'(x) \ne 0 $$

Y así sucesivamente.