Función constante en un intervalo
Una función f(x) es una función constante en un intervalo [a,b] si y solo si es derivable en [a,b] y su primera derivada es nula en todos los puntos de dicho intervalo. $$ \forall x \in [a,b] \:\:\:\:\: f'(x)=0 $$
A este resultado se le conoce como el Teorema de Caracterización de las Funciones Constantes.
Un ejemplo práctico
Consideremos las siguientes funciones constantes:
$$ f(x) = 2 \\ g(x)=3 $$
Para cualquier valor de x, f(x) toma siempre el valor 2, mientras que g(x) toma siempre el valor 3.
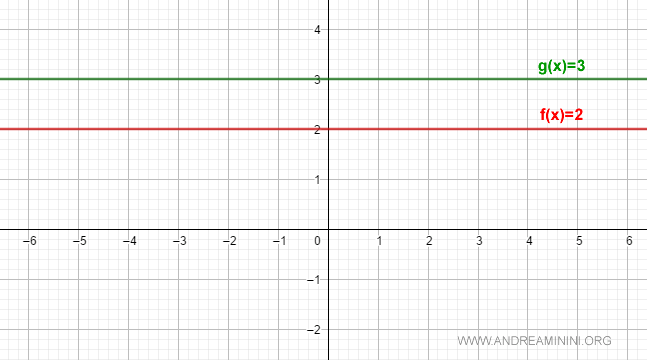
Las derivadas de f(x) y g(x) son en ambos casos iguales a cero:
$$ f'(x) = 0 \\ g'(x)=0 $$
Esto se debe a que la derivada de una constante k es siempre cero:
$$ \frac{d k}{d x} = 0 $$
Demostración y explicación
1] Una función constante tiene derivada nula
Supongamos que f(x) es constante en todo el intervalo [a,b]:
$$ f(x) = c $$
Para calcular la derivada, aplicamos el límite del cociente incremental cuando h → 0 en un punto cualquiera x ∈ [a,b]. Este procedimiento nos conduce a la primera derivada de f(x):
$$ f'(x)= \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} $$
Como f(x) es constante, tenemos:
$$ f(x)=c \\ f(x+h)=c $$
Sustituyendo estos valores en el cociente incremental resulta:
$$ f'(x)= \lim_{h \rightarrow 0} \frac{c-c}{h} $$
$$ f'(x)= \lim_{h \rightarrow 0} \frac{0}{h} $$
De modo que, al tender h a cero, el límite se mantiene en cero:
$$ f'(x)= 0 $$
2] Una función con derivada nula es constante
Si una función es derivable en [a,b] y su derivada se anula en todos los puntos del intervalo:
$$ f'(x) = 0 $$
entonces satisface de manera simultánea ambos criterios de monotonía:
$$ \begin{cases} f'(x) \ge 0 \\ f'(x) \le 0 \end{cases} $$
Es decir, la función es al mismo tiempo no decreciente y no creciente en todo [a,b].
Si tomamos un punto cualquiera x > a dentro del intervalo:
$$ x > a $$
la función f(x) debe verificar simultáneamente:
$$ \begin{cases} f(x) \ge f(a) \\ f(x) \le f(a) \end{cases} $$
La única solución posible es:
$$ f(x) = f(a) $$
En consecuencia, para cualquier x > a se cumple que f(x) coincide con f(a).
Así queda demostrado que una función constante tiene derivada nula y, recíprocamente, que una función cuya derivada se anula en todo un intervalo es necesariamente constante.
Y así sucesivamente.