Ejemplo Resuelto - Análisis de Funciones 4

En este ejemplo vamos a analizar la siguiente función:

$$ f(x) = \frac{x}{x^2 + 2} $$

Dominio

La función está definida para todos los números reales:

$$ D_f = (-\infty, +\infty) $$

Puntos no definidos

No existen valores excluidos del dominio, ya que el denominador \( x^2 + 2 \) nunca se anula en los números reales:

$$ x^2 + 2 = 0 \quad \Rightarrow \quad x^2 = -2 $$

Comportamiento asintótico

Estudiemos ahora el comportamiento de la función en el infinito:

$$ \lim_{x \to +\infty} \frac{x}{x^2 + 2} = 0^+ $$

$$ \lim_{x \to -\infty} \frac{x}{x^2 + 2} = 0^- $$

Por tanto, la función tiende a cero por valores positivos cuando \( x \to +\infty \), y a cero por valores negativos cuando \( x \to -\infty \):

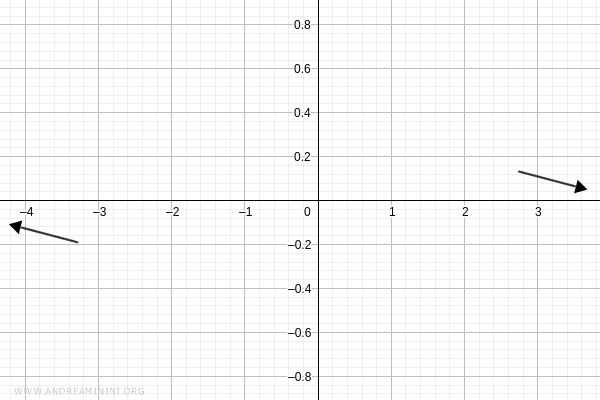
Intersecciones con los ejes

En \( x = 0 \), la función vale:

$$ f(0) = \frac{0}{0^2 + 2} = 0 $$

De este modo, la gráfica pasa por el origen \( (0, 0) \):

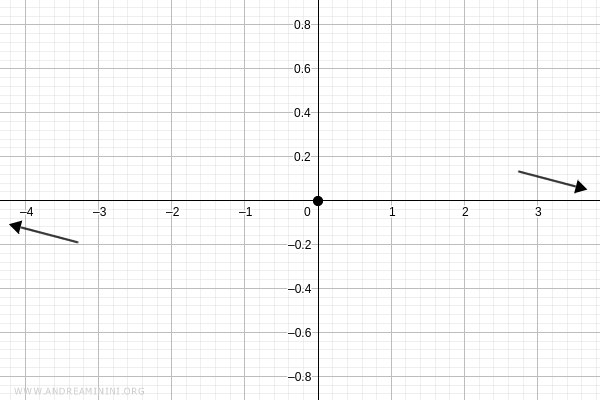
Análisis de signos

La función es negativa en \( (-\infty, 0) \) y positiva en \( (0, +\infty) \):

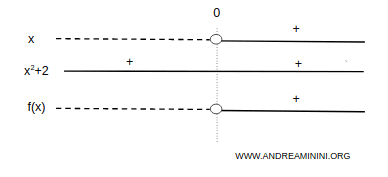
Por lo tanto, en la representación gráfica se descartan las zonas del plano donde la función no toma valores:

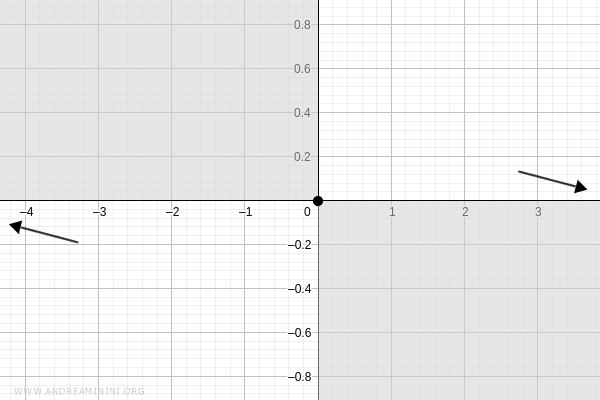
Monotonía

Calculemos la primera derivada:

$$ f'(x) = D\left[ \frac{x}{x^2 + 2} \right] = \frac{(x^2 + 2) - x(2x)}{(x^2 + 2)^2} = \frac{-x^2 + 2}{(x^2 + 2)^2} $$

El estudio del signo de \( f'(x) \) muestra:

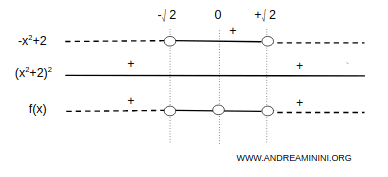
La función crece en \( (-\sqrt{2}, \sqrt{2}) \), y decrece en \( (-\infty, -\sqrt{2}) \) y \( (\sqrt{2}, +\infty) \):

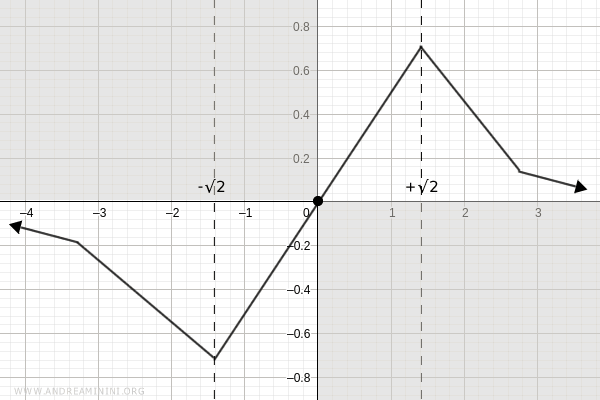
En consecuencia, se obtiene un mínimo local en \( x = -\sqrt{2} \) y un máximo local en \( x = \sqrt{2} \):

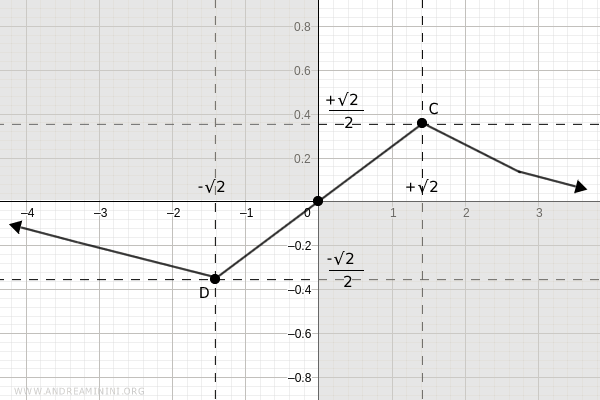
$$ C: \ (x, y) = \left( \sqrt{2}, \frac{ \sqrt{2} }{ (\sqrt{2})^2 + 2 } \right) = \left( \sqrt{2}, \frac{ \sqrt{2} }{4} \right) $$

$$ D: \ (x, y) = \left( -\sqrt{2}, \frac{ -\sqrt{2} }{ (\sqrt{2})^2 + 2 } \right) = \left( -\sqrt{2}, -\frac{ \sqrt{2} }{4} \right) $$

Esto permite afinar la representación de la gráfica:

Concavidad y convexidad

Calculemos ahora la segunda derivada para analizar la concavidad:

$$ f''(x) = D\left[ \frac{ -x^2 + 2 }{ (x^2 + 2)^2 } \right] $$

$$ = \frac{ -2x(x^2 + 2)^2 - 2(x^2 + 2)(-x^2 + 2)(2x) }{ (x^2 + 2)^4 } $$

$$ = \frac{ -2x(x^2 + 2) - 4x(-x^2 + 2) }{ (x^2 + 2)^3 } $$

$$ = \frac{ -2x^3 - 4x + 4x^3 - 8x }{ (x^2 + 2)^3 } $$

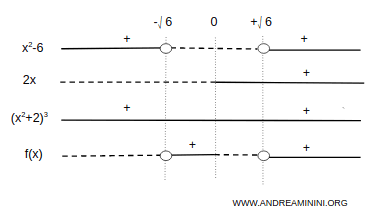
$$ = \frac{ 2x(x^2 - 6) }{ (x^2 + 2)^3 } $$

De aquí se deduce que la función es cóncava en \( (-\infty, -\sqrt{6}) \) y en \( (0, \sqrt{6}) \), y convexa en \( (-\sqrt{6}, 0) \) y en \( (\sqrt{6}, +\infty) \):

La curva adopta, por tanto, la siguiente forma:

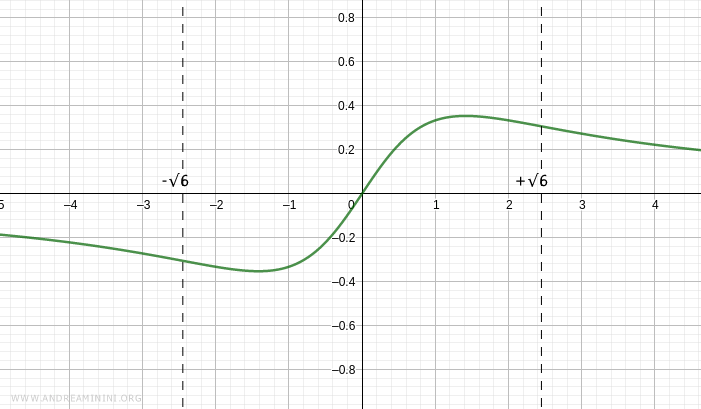
Se obtienen dos puntos de inflexión en \( x = -\sqrt{6} \) y \( x = \sqrt{6} \):

$$ A: \ (x, y) = \left( \sqrt{6}, \frac{ \sqrt{6} }{ (\sqrt{6})^2 + 2 } \right) = \left( \sqrt{6}, \frac{ \sqrt{6} }{8} \right) $$

$$ B: \ (x, y) = \left( -\sqrt{6}, \frac{ -\sqrt{6} }{ (\sqrt{6})^2 + 2 } \right) = \left( -\sqrt{6}, -\frac{ \sqrt{6} }{8} \right) $$

En la gráfica, estos puntos aparecen representados del siguiente modo:

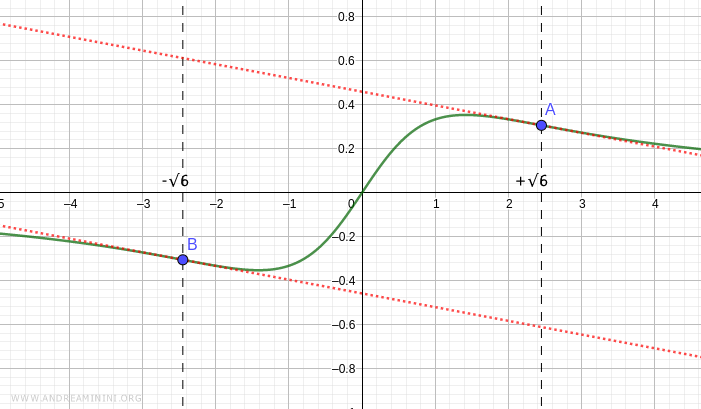
Y así concluye el análisis.