Ejemplo Resuelto de Análisis de Funciones 3

En este ejemplo vamos a estudiar la siguiente función:

$$ f(x) = \frac{x^2 + 2}{x} $$

Dominio

La función está definida para todos los números reales excepto en $ x = 0 $, donde el denominador se anula:

$$ D_f = (-\infty, 0) \cup (0, +\infty) $$

Puntos no definidos

El punto $ x = 0 $ no pertenece al dominio y corresponde a una asíntota vertical.

Calculemos los límites laterales:

$$ \lim_{x \to 0^+} \frac{x^2 + 2}{x} = +\infty $$

$$ \lim_{x \to 0^-} \frac{x^2 + 2}{x} = -\infty $$

Por lo tanto, cuando $ x \to 0 $, la función tiende a $ +\infty $ por la derecha y a $ -\infty $ por la izquierda:

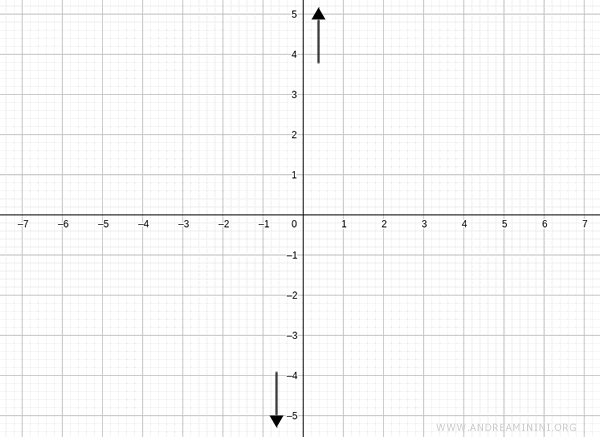
asíntota vertical en x = 0

Comportamiento asintótico

Veamos ahora los límites cuando $ x \to +\infty $ y $ x \to -\infty $:

$$ \lim_{x \to +\infty} \frac{x^2 + 2}{x} = +\infty $$

$$ \lim_{x \to -\infty} \frac{x^2 + 2}{x} = -\infty $$

Así, cuando $ x \to +\infty $, $ f(x) \to +\infty $, y cuando $ x \to -\infty $, $ f(x) \to -\infty $:

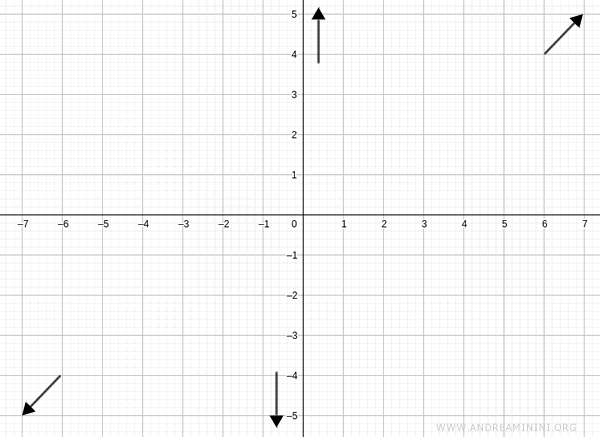
comportamiento asintótico en el infinito

Intersecciones con los ejes

En $ x = 0 $, la función no está definida:

$$ f(0) = \frac{0^2 + 2}{0} $$

Para determinar posibles cortes con el eje x, resolvemos:

$$ \frac{x^2 + 2}{x} = 0 $$

Multiplicamos ambos lados por $ x $:

$$ x^2 + 2 = 0 $$

$$ x^2 = -2 $$

Como la ecuación no tiene soluciones reales, la gráfica no corta el eje x.

Análisis de signos

La función es negativa en $ (-\infty, 0) $ y positiva en $ (0, +\infty) $:

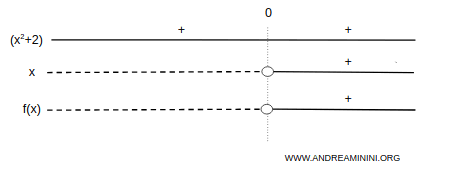
análisis de signos

Por tanto, podemos descartar las zonas del plano donde la función no toma valores (áreas sombreadas):

áreas sombreadas

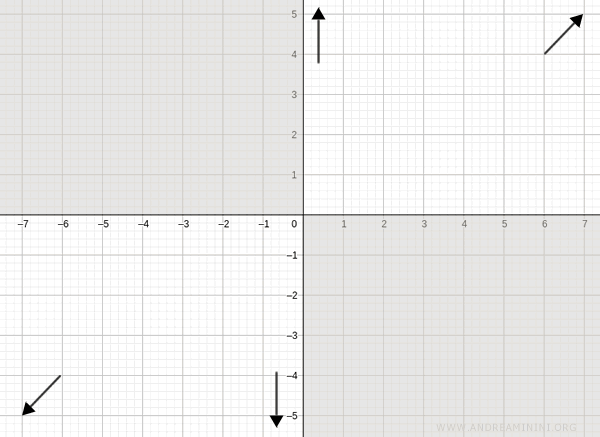
Monotonía

Calculemos la primera derivada:

$$ f'(x) = D\left[ \frac{x^2 + 2}{x} \right] = \frac{2x \cdot x - (x^2 + 2)}{x^2} = \frac{x^2 - 2}{x^2} $$

Estudiamos el signo de $ f'(x) $:

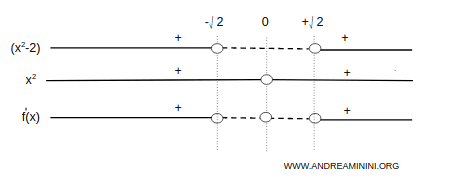
signo de la primera derivada

La función es creciente en $ (-\infty, -\sqrt{2}) $ y en $ (\sqrt{2}, +\infty) $, y decreciente en $ (-\sqrt{2}, \sqrt{2}) $:

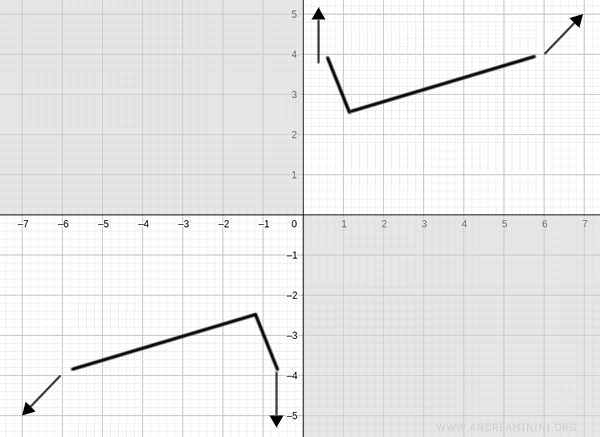
monotonía

En $ x = -\sqrt{2} $, la función alcanza un máximo local, ya que $ f'(x) = 0 $ y la derivada cambia de positiva a negativa:

$$ \left( -\sqrt{2}, f(-\sqrt{2}) \right) = \left( -\sqrt{2}, \frac{(-\sqrt{2})^2 + 2}{-\sqrt{2}} \right) = \left( -\sqrt{2}, -\frac{4}{\sqrt{2}} \right) $$

En $ x = \sqrt{2} $, la función presenta un mínimo local, porque $ f'(x) = 0 $ y la derivada cambia de negativa a positiva:

$$ \left( \sqrt{2}, f(\sqrt{2}) \right) = \left( \sqrt{2}, \frac{(\sqrt{2})^2 + 2}{\sqrt{2}} \right) = \left( \sqrt{2}, \frac{4}{\sqrt{2}} \right) $$

Concavidad y convexidad

Calculemos ahora la segunda derivada:

$$ f''(x) = D\left[ \frac{x^2 - 2}{x^2} \right] $$

$$ = \frac{2x(x^2) - (x^2 - 2)(2x)}{x^4} = \frac{4x}{x^4} = \frac{4}{x^3} $$

La función es cóncava en $ (-\infty, 0) $ y convexa en $ (0, +\infty) $:

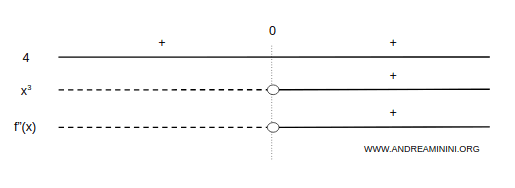
concavidad y convexidad

La gráfica de la función, en consecuencia, tiene la siguiente forma:

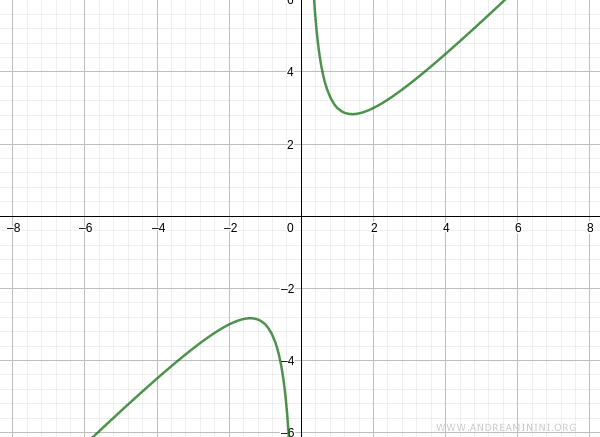
gráfica de la función

Asíntotas oblicuas

Analicemos ahora la posible existencia de asíntotas oblicuas.

Primero calculamos la pendiente $ m $:

$$ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x^2 + 2}{x^2} = 1 $$

Como $ m $ es finito, calculamos $ q $:

$$ q = \lim_{x \to +\infty} \left( f(x) - m x \right) = \lim_{x \to +\infty} \left( \frac{x^2 + 2}{x} - x \right) = \lim_{x \to +\infty} \frac{2}{x} = 0 $$

De este modo, la función tiene una asíntota oblicua cuando $ x \to +\infty $, dada por:

$$ y = x $$

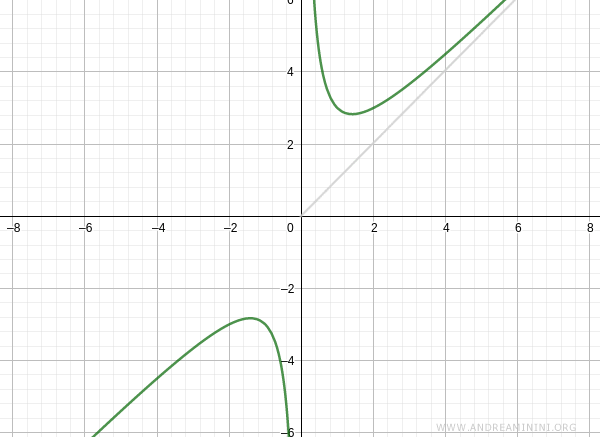
asíntota oblicua

Repitiendo el mismo procedimiento para $ x \to -\infty $:

$$ m = \lim_{x \to -\infty} \frac{f(x)}{x} = 1 $$

$$ q = \lim_{x \to -\infty} \left( f(x) - m x \right) = \lim_{x \to -\infty} \frac{2}{x} = 0 $$

La asíntota oblicua vuelve a ser:

$$ y = x $$

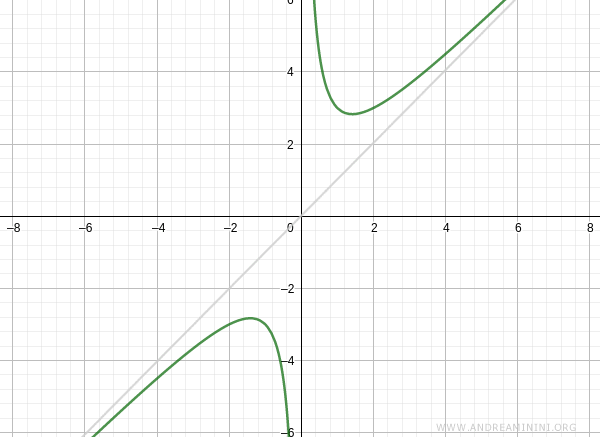
asíntota oblicua

Y así sucesivamente.