El límite de una función
- El límite de una función f(x) cuando x se aproxima a un punto x0
- Convergente, si l es un número finito.
- Divergente, si l es infinito.
- Inexistente, si la función oscila o el límite simplemente no existe en x0.
$$ \lim_{x \rightarrow x_0} f(x) = l $$ puede clasificarse en tres categorías:
En esta definición, x0 es un punto de acumulación del dominio de f(x), y l puede ser cualquier número real, tanto finito como infinito.
Límite convergente
A] Cuando x0 es un número finito
Decimos que el límite de f(x) cuando x tiende a x0 es igual a l
$$ \lim_{x \rightarrow x_0} f(x) = l $$ si, para todo ε > 0, existe un δ > 0 tal que:
$$ l - \epsilon < f(x) < l + \epsilon $$ para todo x en el intervalo (x0 - δ, x0 + δ).
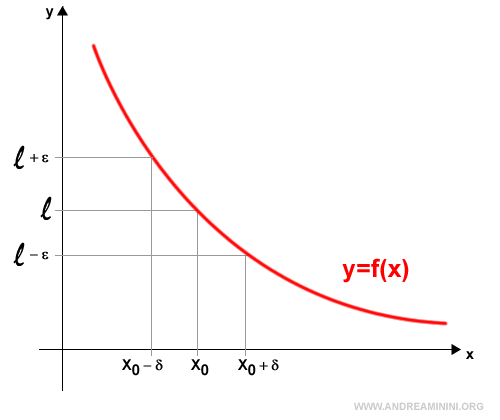
En este caso, l representa un número real finito, y la función se aproxima progresivamente a ese valor a medida que x se acerca a x0.
En forma simbólica:
$$ \lim_{x \rightarrow x_0} f(x) = l \Leftrightarrow \forall \ \epsilon>0 \ , \ \exists \ \delta>0: |f(x)-l|<\epsilon \ , \ \forall \ x \in I: 0 \ne |x-x_0|<\delta $$
En otras palabras, se dice que una función tiene un límite real \( l \) cuando \( x \) tiende a \( x_0 \) si, para todo número real positivo \( \epsilon \), existe un entorno perforado \( I \) de \( x_0 \) tal que se cumple \( |f(x) - l| < \epsilon \) para todo \( x \in I \) con \( x \neq x_0 \).
El punto \( x_0 \) es un punto de acumulación y, como tal, puede pertenecer o no al entorno \( I \).
Por consiguiente, una función \( f(x) \) puede admitir un límite real finito \( l \) cuando \( x \) tiende a \( x_0 \), incluso en el caso de que no esté definida en el punto \( x_0 \).
Nota. El límite de una función también puede entenderse a partir de sus subsucesiones. Si toda sucesión xn en el dominio A que converge a x0 cumple que f(xn) → l, entonces el límite de f(x) en x0 es l.
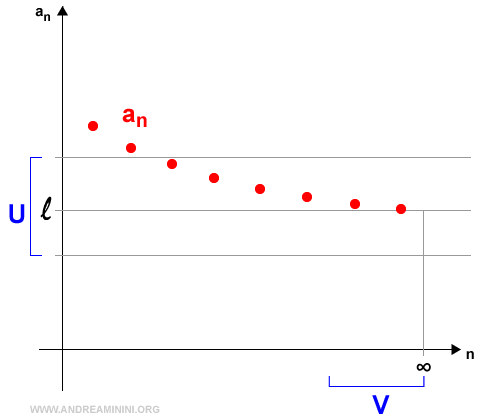
B] Cuando x0 tiende a infinito positivo o negativo
El límite de f(x) cuando x tiende a infinito es igual a un valor finito l
$$ \lim_{x \rightarrow \infty} f(x) = l $$ si, para todo ε > 0, existe un número k > 0 tal que:
$$ |f(x) - l| < \epsilon $$ para todo x > k.
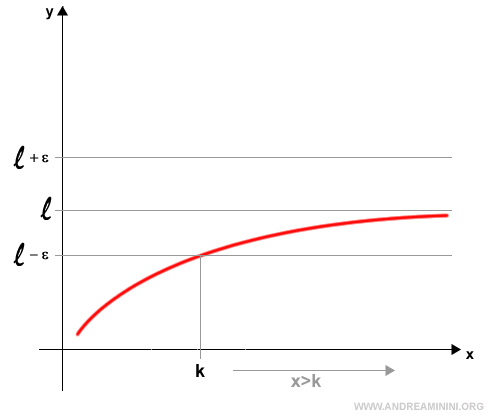
Esto significa que, aunque x crezca sin límite, f(x) se acerca cada vez más a un valor constante l.
Formalmente:
$$ \lim_{x \rightarrow \infty} f(x) = l \Leftrightarrow \forall \epsilon>0, \exists k>0: |f(x)-l|<\epsilon, \forall x>k $$
La misma idea se aplica cuando x tiende a -∞.
Ejemplo. Para la función f(x) = 1/x:
$$ \lim_{x \rightarrow +\infty} \frac{1}{x} = 0 $$
A medida que x aumenta, el valor de 1/x se acerca cada vez más a cero.
Límite divergente hacia el infinito
A] Si x0 es un número finito
El límite de una función cuando x→x0 diverge a infinito positivo $$ \lim_{x \rightarrow x_0} f(x) = +∞ $$ si, para todo número real M>0, existe un número δ>0 tal que la función f(x) toma valores mayores que M para todo x en el entorno x0-δ<x<x0+δ.
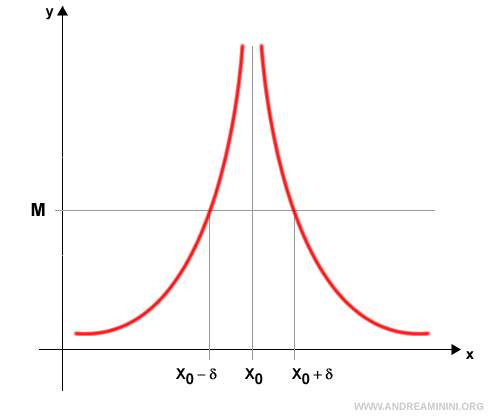
En forma simbólica $$ \lim_{x \rightarrow x_0} f(x) = +∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)>M, \forall x \in A: 0 \ne |x-x_0|<δ $$ En otras palabras, al restringir x a un entorno suficientemente pequeño de $ x_0 $, los valores de la función $ f(x) $ acaban superando cualquier cota positiva previamente fijada.
El límite puede divergir tanto a infinito positivo (+∞) como a infinito negativo (-∞).
La función f(x) diverge a infinito negativo $$ \lim_{x \rightarrow x_0} f(x) = -∞ $$ si, para todo número real M>0, existe un número δ>0 tal que la función f(x) toma valores menores que -M para todo x en el entorno x0-δ<x<x0+δ.
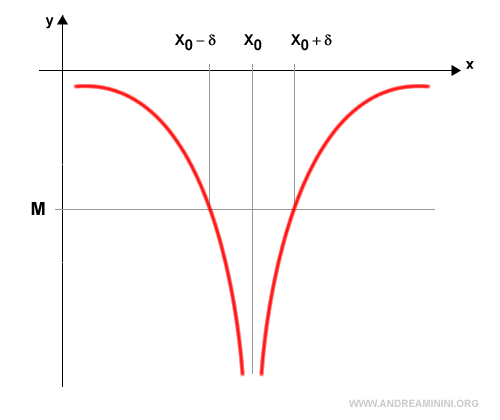
En forma simbólica
$$ \lim_{x \rightarrow x_0} f(x) = -∞ \Leftrightarrow \forall M>0, \exists δ>0: f(x)<-M, \forall x \in A: 0 \ne |x-x_0|<δ $$
Es decir, cuando x se considera suficientemente próximo a $ x_0 $, los valores de la función $ f(x) $ terminan situándose por debajo de cualquier cota negativa prescrita.
Ejemplo. Dada la función f(x)=1/((x-1)^2), calcúlese el límite cuando x→1. $$ \lim_{x \rightarrow 1} \frac{1}{(x-1)^2} = +∞ $$
B] Cuando x tiende a infinito positivo o negativo
El límite de una función cuando x→+∞ diverge a infinito positivo $$ \lim_{x \rightarrow +∞} f(x) = +∞ $$ si, para todo número real M>0, existe un número k>0 tal que la función f(x) toma valores mayores que M para todo x>k.
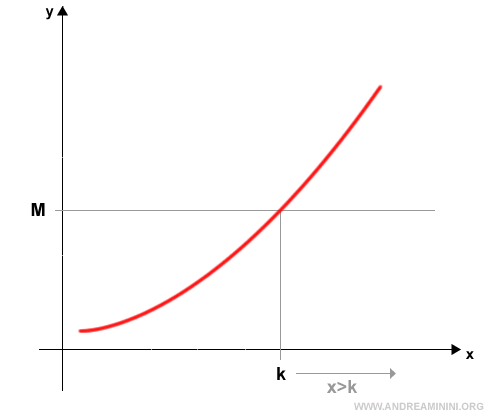
En forma simbólica $$ \lim_{x \rightarrow +∞} f(x) = +∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)>M, \forall x>k $$ Dicho de otro modo, a medida que $ x $ crece sin límite, los valores de la función superan cualquier cota positiva fijada y continúan aumentando indefinidamente.
Un límite puede divergir tanto a infinito positivo (+∞) como a infinito negativo (-∞).
El límite de una función cuando x→+∞ diverge a infinito negativo $$ \lim_{x \rightarrow +∞} f(x) = -∞ $$ si, para todo número real M>0, existe un número k>0 tal que la función f(x) toma valores menores que -M para todo x>k.
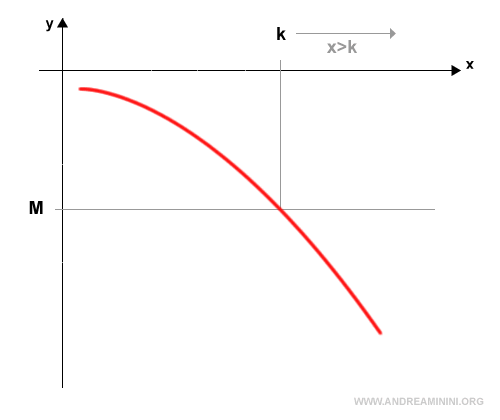
En forma simbólica $$ \lim_{x \rightarrow +∞} f(x) = -∞ \Leftrightarrow \forall M>0, \exists k>0: f(x)<-M, \forall x>k $$
Es decir, cuando $ x $ aumenta sin restricción, los valores de la función acaban quedando por debajo de cualquier cota negativa establecida y siguen disminuyendo sin límite inferior.
Ejemplo. Dada la función f(x)=x2, calcúlese el límite cuando x→+∞. $$ \lim_{x \rightarrow +∞} x^2 = +∞ $$
En estos ejemplos se ha considerado únicamente el caso en el que x tiende a infinito positivo. La definición del límite cuando x→-∞ se obtiene de forma completamente análoga.
Límite inexistente
A] Cuando x0 es un número finito
El límite de f(x) en x0 no existe si los límites laterales no coinciden:
$$ \lim_{ x \rightarrow x_0^+ } f(x) \ne \lim_{ x \rightarrow x_0^- } f(x) $$
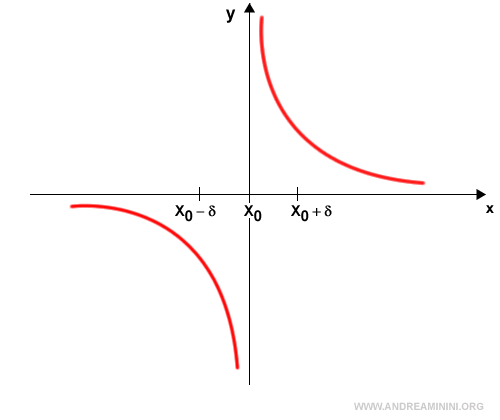
Esto ocurre, por ejemplo, cuando la función presenta una discontinuidad o una asíntota vertical en x0.
B] Cuando x0 tiende a infinito positivo o negativo
El límite de una función cuando x → ±∞ no existe si la función oscila sin estabilizarse o no tiende a ningún valor definido:
$$ \lim_{ x \rightarrow \pm \infty } f(x) = \text{no existe} $$
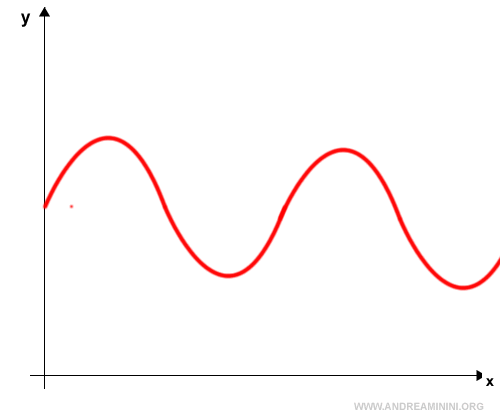
Ejemplo
Para la función:
$$ f(x) = \frac{1}{x} $$
El límite cuando x → 0 no existe, porque los límites laterales son distintos:
$$ \lim_{ x \rightarrow 0^+ } \frac{1}{x} = +\infty $$
$$ \lim_{ x \rightarrow 0^- } \frac{1}{x} = -\infty $$
La función 1/x no está definida en x = 0 y presenta una asíntota vertical en ese punto.
En resumen, el estudio de los límites permite comprender cómo se comportan las funciones cerca de ciertos valores o cuando x crece sin límite. Esta noción es esencial para definir la continuidad, las derivadas y muchos otros conceptos fundamentales del análisis matemático.