Teorema de Weierstrass

Si una función f(x) es continua en un intervalo cerrado y acotado [a,b], entonces alcanza un mínimo absoluto m = f(x₁) y un máximo absoluto M = f(x₂). En otras palabras, siempre existen dos puntos dentro del intervalo donde la función toma sus valores extremo. $$ f(x_1) \le f(x) \le f(x_2) \:\:\: \forall x \in [a,b] $$

Los puntos \( x_1 \) y \( x_2 \) reciben el nombre de mínimo absoluto y máximo absoluto. Este resultado es fundamental en análisis matemático: nos asegura que, bajo las condiciones adecuadas, una función no solo está acotada, sino que además alcanza efectivamente sus cotas.

Conviene recordar que la condición es suficiente pero no necesaria. Existen funciones que alcanzan máximos o mínimos aun sin cumplir las hipótesis del teorema, pero en esos casos no hay garantía.

Nota. El teorema también se aplica a funciones de varias variables siempre que el dominio sea compacto, es decir, cerrado y acotado, y la función sea continua.

Un ejemplo práctico

Tomemos la función

$$ f(x) = \frac{1}{x} $$

Sobre el intervalo (0,5] esta función no tiene máximo absoluto. A medida que x se acerca a cero, f(x) crece sin límite. Tampoco posee mínimo absoluto en [5,+∞) porque, aunque se aproxima a cero, nunca llega a alcanzarlo.

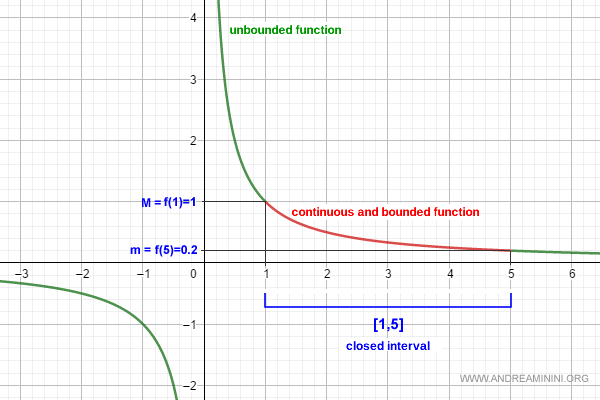
La situación cambia si restringimos el dominio al intervalo cerrado [1,5]. En este caso la función queda claramente acotada:

$$ 0.2 \le f(x) \le 1 $$

Ahora sí aparecen el máximo y el mínimo absolutos:

$$ M = f(1) = 1 $$

$$ m = f(5) = 0.2 $$

Nota. En este ejemplo los extremos se encuentran en los puntos extremos del intervalo, pero no siempre sucede así. Muchas funciones alcanzan sus valores máximo o mínimo dentro del propio intervalo.

Cómo se demuestra el teorema

Supongamos que f(x) es continua en el intervalo cerrado [a,b] y que su supremo es M. El objetivo es mostrar que ese supremo se alcanza realmente en algún punto.

$$ M = sup(f(x): x \in [a,b]) $$

Ejemplo. La función coseno en el intervalo [-1,1] alcanza su máximo absoluto en \( x_0 = 0 \), donde vale 1.

Como M es una cota superior, podemos construir una sucesión de puntos \( x_n \) donde los valores de la función se aproximan cada vez más a M:

$$ \lim_{n \rightarrow \infty;} f(x_n) = M $$

A partir de aquí se distinguen dos casos:

1. M es infinito: si los valores de f(x) pueden crecer sin límite, la sucesión diverge y M = +∞.
2. M es finito: para cada n existe un punto \( x_n \) tal que $$ M - \frac{1}{n} < f(x_n) \le M $$. Entonces la sucesión converge hacia un valor finito.

Para aclarar qué ocurre realmente, usamos una propiedad esencial: como [a,b] es un intervalo acotado, cualquier sucesión dentro de él tiene una subsucesión convergente, según el teorema de Bolzano - Weierstrass.

Ejemplo. Una subsucesión convergente dentro de un intervalo acotado.

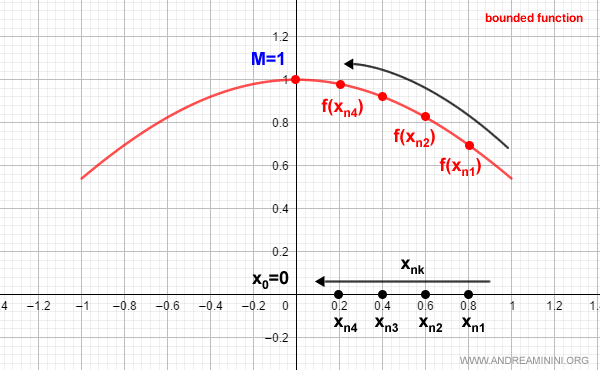
Sea \( x_{nk} \) una subsucesión que converge a un punto \( x_0 \) en [a,b]:

$$ \lim_{n \rightarrow \infty;} x_{nk} = x_0 $$

Dado que f es continua, los valores funcionales también convergen:

$$ \lim_{n \rightarrow \infty;} f(x_{nk}) = f(x_0) $$

Esto nos lleva a la conclusión central:

$$ M = f(x_0). $$

El supremo se alcanza realmente y coincide con el máximo absoluto de la función en el intervalo.

$$ M = f(x_0) = sup \{ f(x) : x \in [a,b] \} $$

Nota. Para el mínimo absoluto el razonamiento es idéntico, sustituyendo el supremo por el ínfimo.

Weierstrass en funciones de varias variables

Si \( A \subseteq \mathbb{R}^n \) es un conjunto compacto y \( f : A \to \mathbb{R} \) es continua, entonces f alcanza un mínimo absoluto y un máximo absoluto en A. Es decir: \[f(x_{\text{min}}) \le f(x) \le f(x_{\text{max}}) \quad \forall x \in A.\]

Esta versión multivariable no añade dificultad conceptual: basta con que el dominio sea cerrado y acotado para garantizar la existencia de extremos absolutos.

Nota. Para funciones de una variable el dominio típico es un intervalo cerrado. En dos variables podemos tener, por ejemplo, un disco cerrado \( x^2 + y^2 \le r^2 \), cuya frontera corresponde a su circunferencia exterior.

Ejemplo

Consideremos la función

\[ f(x,y) = x^2 + y^2 \]

definida en el disco cerrado de radio 1:

\[ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \le 1 \} \]

El dominio A es compacto, y la función es continua en toda la región.

El mínimo absoluto aparece en el centro del disco, donde \( f(0,0) = 0 \).

El máximo absoluto se alcanza sobre toda la circunferencia exterior, donde \( x^2 + y^2 = 1 \) y \( f(x,y) = 1 \). Hay infinitos puntos de máximo absoluto.

Este mismo razonamiento se aplica a cualquier función continua definida sobre un dominio compacto. La compacidad garantiza que los extremos existen, independientemente de la complejidad de la función.