Teorema sobre el límite de las sucesiones monótonas

Una sucesión monótona tiene siempre un límite, que puede ser finito o infinito. $$ \lim_{n \rightarrow \infty} a_n = \begin{cases} l \\ \infty \end{cases} $$ Si además la sucesión está acotada, entonces necesariamente converge a un valor finito. $$ \lim_{n \rightarrow \infty} a_n = l $$

Este resultado es fundamental en análisis matemático. Nos dice que las sucesiones que avanzan siempre en la misma dirección, sin oscilar ni retroceder, poseen un comportamiento límite claro: o se estabilizan en un valor concreto o crecen sin límite. Por esta razón, toda sucesión monótona es también una sucesión regular.

Conceptos clave. Una sucesión es monótona cuando cada término a_n es siempre mayor o igual que el siguiente a_n+1, o siempre menor o igual. Si la desigualdad es estricta, la sucesión es estrictamente monótona. Una sucesión es regular cuando tiene un límite (finito o infinito). Por último, una sucesión está acotada si todos sus términos permanecen dentro de límites superior e inferior fijos.

Ejemplos ilustrativos

Ejemplo 1

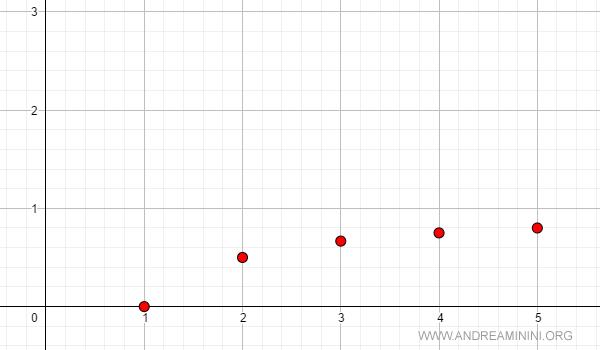
Consideremos la sucesión monótona creciente

$$ a_n = \frac{n-1}{n} $$

En este caso, todos los términos se acercan a 1 al aumentar n:

$$ \lim_{n \rightarrow \infty} a_n = 1 $$

Representación gráfica:

Ejemplo 2

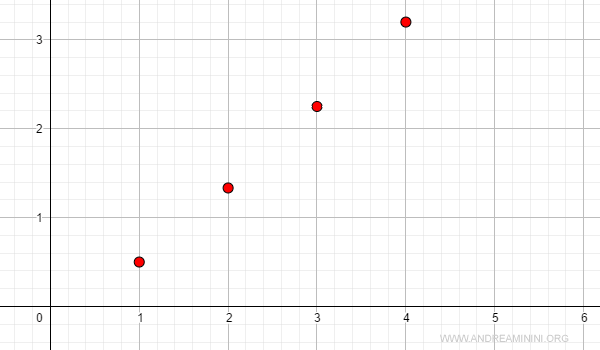
Ahora observemos la sucesión

$$ a_n = \frac{n^2}{n+1} $$

Es también monótona creciente, pero en este caso los valores aumentan sin límite:

$$ \lim_{n \rightarrow \infty} a_n = +\infty $$

Representación gráfica:

 

Demostración del teorema

Para justificar el resultado, distinguimos dos casos: sucesiones monótonas acotadas y sucesiones monótonas no acotadas.

Caso 1: sucesión creciente y acotada

Sea una sucesión monótona, creciente y acotada. Para cualquier ε > 0 existe un índice v tal que, para todo n > v, se cumple:

$$ l - \epsilon < a_v \le a_n \le l < l + \epsilon $$

En el plano cartesiano esta situación se visualiza así:

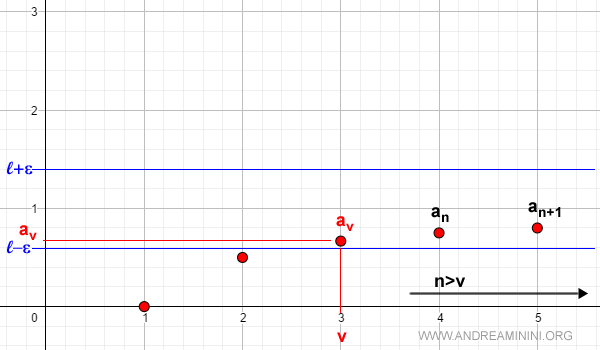
Esto demuestra que, al crecer n, la sucesión converge a l = 1:

$$ \lim_{n \rightarrow \infty} a_n = 1 $$

Caso 2: sucesión creciente y no acotada

Supongamos ahora que la sucesión es monótona creciente y no acotada. En ese caso, para cualquier número M > 0, es posible encontrar un índice v tal que, para todo n > v:

$$ a_n \ge a_v > M $$

Gráficamente, la tendencia creciente e ilimitada se aprecia así:

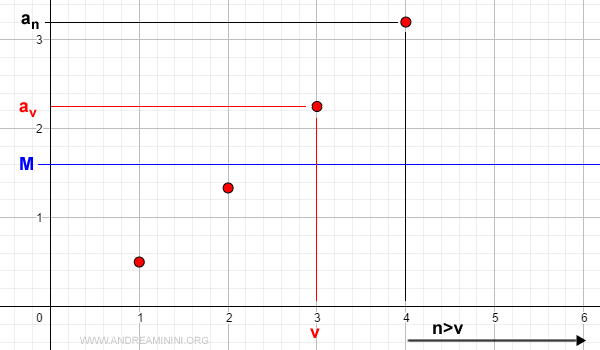
Por tanto, la sucesión diverge:

$$ \lim_{n \rightarrow \infty} a_n = +\infty $$

Nota. Para las sucesiones monótonas decrecientes se aplica el mismo razonamiento. Si está acotada, converge; si no lo está, diverge.