Sucesiones monótonas crecientes y decrecientes
En matemáticas, una sucesión monótona es aquella cuyos términos avanzan siempre en la misma dirección: crecen o decrecen sin retroceder. Analizar su comportamiento nos permite entender mejor cómo evolucionan las series numéricas y hacia qué valores tienden.
- Estríctamente creciente
Cada término es mayor que el anterior: $$ a_{n+1} > a_n $$ - No decreciente
Cada término es mayor o igual que el anterior: $$ a_{n+1} \ge a_n $$ - Estríctamente decreciente
Cada término es menor que el anterior: $$ a_{n+1} < a_n $$ - No creciente
Cada término es menor o igual que el anterior: $$ a_{n+1} \le a_n $$
Algunos libros utilizan expresiones como “creciente en sentido amplio” o “decreciente en sentido amplio” para referirse a los casos no estrictos. Las diferencias son pequeñas, pero conviene tenerlas claras cuando se estudian los límites de una sucesión.
Nota. Una sucesión constante es aquella en la que todos los términos son iguales: $$ a_{n+1} = a_n $$. Este tipo de sucesión puede considerarse tanto creciente como decreciente, ya que no presenta cambios entre sus valores.
Ejemplo práctico
Ejemplo 1: Sucesión estrictamente decreciente
Consideremos la sucesión:
$$ a_n = \frac{1}{n} $$
Al aumentar n, los términos se hacen cada vez más pequeños, ya que:
$$ a_{n+1} < a_n $$
$$ \frac{1}{n+1} < \frac{1}{n} $$
En el plano cartesiano, los puntos se aproximan al eje horizontal, lo que muestra claramente su carácter decreciente:
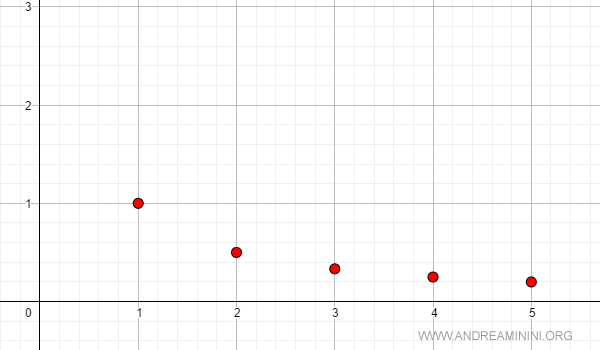
Ejemplo 2: Sucesión estrictamente creciente
Ahora tomemos la sucesión:
$$ a_n = \frac{n-1}{n} $$
En este caso, cada término es mayor que el anterior, porque:
$$ a_{n+1} > a_n $$
y, al comprobarlo, obtenemos:
$$ \frac{n-1+1}{n+1} > \frac{n-1}{n} $$
que se simplifica a:
$$ \frac{n}{n+1} > \frac{n-1}{n} $$
y finalmente a:
$$ \frac{1}{n(n+1)} > 0 $$
En el gráfico se observa cómo los términos se aproximan cada vez más al valor 1, sin llegar a alcanzarlo:
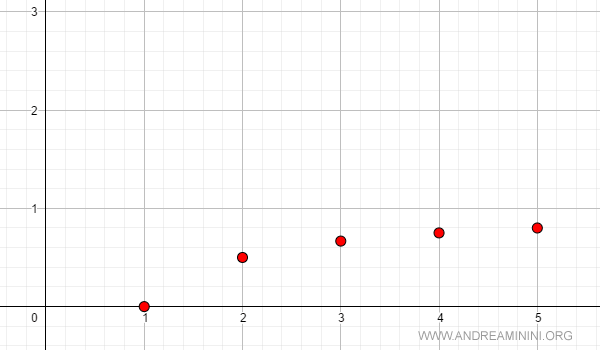
Sucesiones constantes
Una sucesión es constante cuando, para todo n ∈ N: $$ a_{n+1} = a_n $$
Las sucesiones constantes representan un caso límite: no crecen ni decrecen, pero mantienen un valor fijo que puede interpretarse como su propio límite. Son, en cierto modo, el punto de equilibrio dentro del conjunto de las sucesiones monótonas.