Sucesiones convergentes

Una sucesión a_n se denomina convergente cuando su límite, al hacer n→∞, es un número finito l: $$ \lim_{n \rightarrow \infty} a_n = l $$ En otras palabras, para todo ε > 0, existe un número v tal que: $$ l - \epsilon < a_n < l + \epsilon \quad \forall n > v $$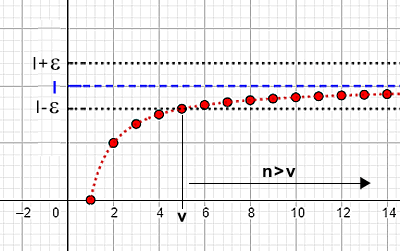
De forma equivalente, esta condición puede expresarse como: $$ | a_n - l | < \epsilon \quad \forall n > v $$

Toda sucesión convergente es también una sucesión acotada.

No obstante, el recíproco no siempre es cierto: una sucesión acotada no tiene por qué ser convergente.

Por ejemplo, la sucesión (-1)ⁿ alterna entre -1 y +1. Está acotada, pero no converge.

Nota. Si una sucesión converge a cero, se denomina sucesión infinitesimal. Se trata de un caso particular de sucesión convergente: $$ \lim_{ n \rightarrow \infty } a_n = 0 $$

Un ejemplo práctico

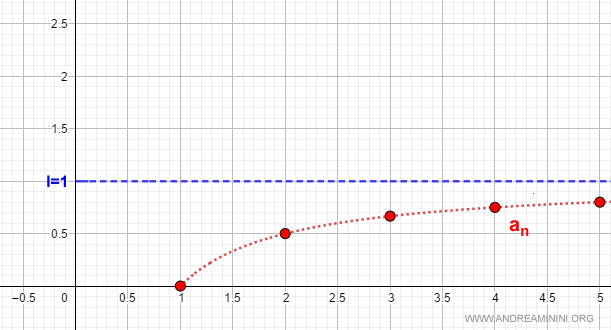
Consideremos la sucesión:

$$ a_n = \frac{n-1}{n} $$

El límite de esta sucesión cuando n→∞ es igual a uno:

$$ \lim_{ n \rightarrow \infty } \frac{n-1}{n} = 1 $$

Por tanto, la sucesión es convergente, ya que su límite cuando n→∞ es un número finito.

Verificación paso a paso

Una sucesión es convergente si, para todo ε > 0, se cumple la condición:

$$ | a_n - l | < \epsilon $$

En este caso, l = 1:

$$ | a_n - 1 | < \epsilon $$

Sabemos que el término general es a_n = (n-1)/n:

$$ \left| \frac{n-1}{n} - 1 \right| < \epsilon $$

Simplifiquemos la expresión paso a paso:

$$ \left| \frac{n-1 - n}{n} \right| < \epsilon $$

$$ \left| \frac{-1}{n} \right| < \epsilon $$

Como n > 0, podemos eliminar el valor absoluto:

$$ \frac{1}{n} < \epsilon $$

Reordenando la desigualdad, obtenemos:

$$ n > \frac{1}{\epsilon} $$

Esto demuestra que, si el índice n supera 1/ε, la diferencia |a_n - l| será efectivamente menor que ε.

Por tanto, el valor umbral v es:

$$ v = \frac{1}{\epsilon} $$

Para todo n > v, se cumple que |a_n - l| < ε, lo cual confirma que la sucesión es convergente.

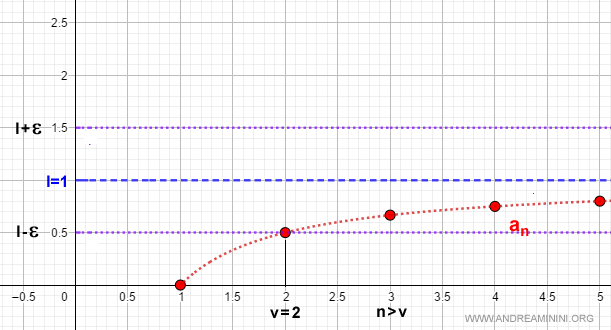
Nota. En el gráfico anterior, ε = 0.5, por lo que v = 1/ε = 1/0.5 = 2. Para todo n > v, es decir, n > 2, los términos de la sucesión a_n permanecen completamente dentro del intervalo (l - ε, l + ε).

Y así sucesivamente.