Sucesiones divergentes

Una sucesión $a_n$ se denomina divergente (o infinita) cuando su límite es igual a $+\infty$. $$ \lim_{ n \rightarrow +\infty } a_n = +\infty $$ En otras palabras, para todo número real positivo $M > 0$, existe un número natural $v$ tal que $a_n > M$ para todo $n > v$: $$ \forall M > 0, \exists v : a_n > M \:\: \forall n > v $$

De manera análoga, una sucesión también se considera divergente si su límite tiende a $-\infty$.

Decimos que una sucesión $a_n$ es divergente negativamente si su límite es $-\infty$: $$ \lim_{ n \rightarrow +\infty } a_n = -\infty $$ Esto significa que, para todo $M > 0$, existe un número natural $v$ tal que $a_n < -M$ para todo $n > v$: $$ \forall M > 0, \exists v : a_n < -M \:\: \forall n > v $$

Ejemplos prácticos

Ejemplo 1

Consideremos la sucesión $a_n = n^2$:

$$ a_n = n^2 $$

Esta sucesión diverge hacia el infinito positivo, ya que su límite cuando $n$ tiende a infinito es $+\infty$:

$$ \lim_{n \rightarrow +\infty} n^2 = +\infty $$

Los primeros términos de la sucesión son: $$ a_n = \{ 1, 4, 9, 16, \dots , +\infty \} $$

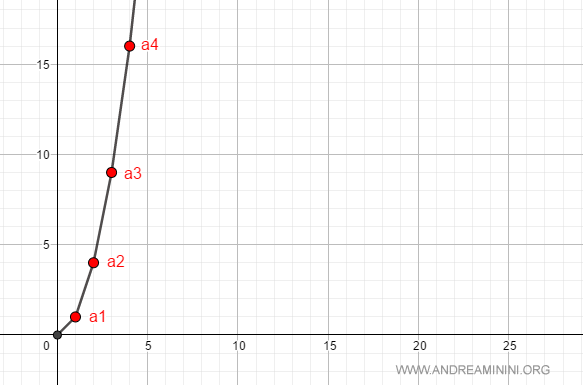
Por ejemplo, si elegimos $M = 10$, existe un número natural $v = 3$ (ya que $a_v = a_3 = 9$) tal que, para todo $n > 3$, se cumple que $a_n > 10$.

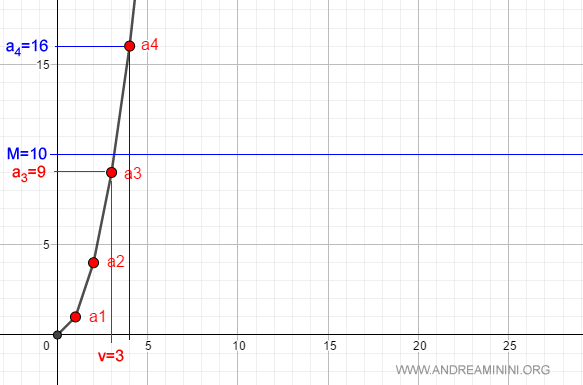
Este razonamiento es válido para cualquier valor positivo de $M$.

Ejemplo 2

Consideremos ahora la sucesión $a_n = 1 - n^2$:

$$ a_n = 1 - n^2 $$

Esta sucesión diverge hacia el infinito negativo, ya que su límite cuando $n$ tiende a infinito es $-\infty$:

$$ \lim_{n \rightarrow +\infty} (1 - n^2) = -\infty $$

Los primeros términos de la sucesión son: $$ a_n = \{ 0, -3, -8, -15, \dots , -\infty \} $$

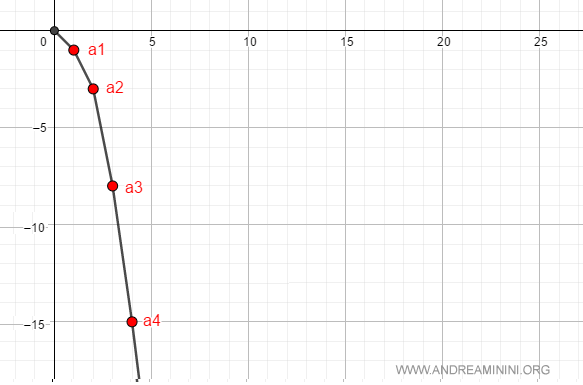
Por ejemplo, si tomamos $M = 10$, existe un número natural $v = 3$ (donde $a_v = a_3 = -9$) tal que, para todo $n > 3$, se cumple $a_n < -M$, es decir, $a_n < -10$.

En efecto, $a_4 = -15 < -10$.

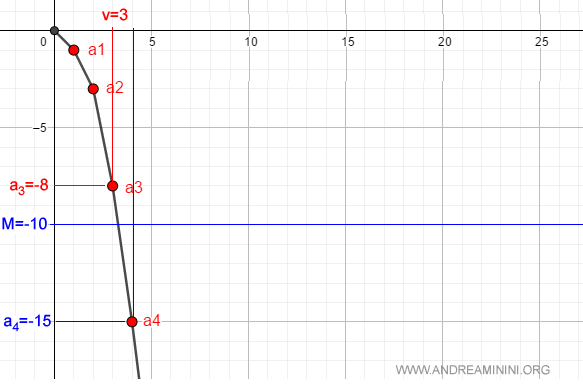
Y el mismo razonamiento puede aplicarse a cualquier otro valor de $M > 0$.