Sucesiones infinitesimales

Una sucesión infinitesimal es una sucesión cuyos términos se hacen cada vez más pequeños hasta acercarse arbitrariamente a cero: $$ \lim_{n \rightarrow \infty} a_n = 0 $$ En otras palabras, aunque nunca llegue exactamente a cero, sus valores pueden ser tan pequeños como queramos si tomamos n lo suficientemente grande.

Un ejemplo sencillo

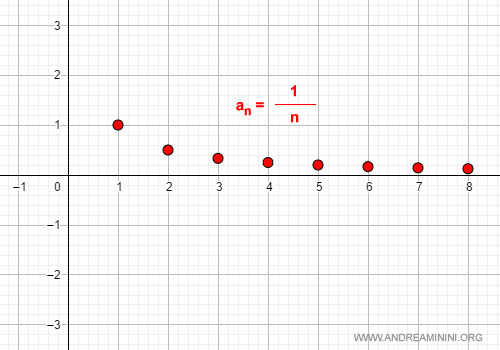
Tomemos como ejemplo la sucesión:

$$ a_n = \frac{1}{n} $$

Cuando n aumenta (por ejemplo, 10, 100, 1 000, 10 000…), los valores de a_n se van haciendo más y más pequeños. Si seguimos este proceso indefinidamente, el resultado se aproxima a cero:

$$ \lim_{n \rightarrow \infty} \frac{1}{n} = 0 $$

Por tanto, podemos afirmar que esta sucesión es infinitesimal.

Propiedades fundamentales

Una sucesión a_n converge a cero si, y solo si, el valor absoluto de sus términos también tiende a cero: $$ \lim_{n \rightarrow \infty} a_n = 0 \Rightarrow \lim_{n \rightarrow \infty} |a_n| = 0 $$

Ejemplo

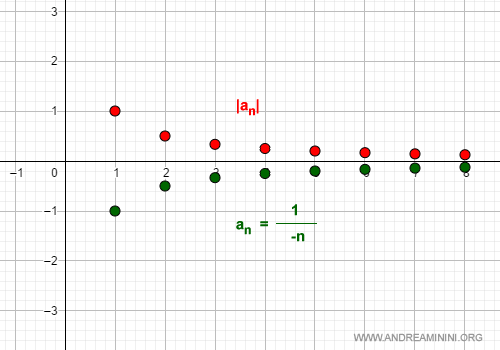
Veamos otro caso similar:

$$ a_n = \frac{1}{-n} $$

Aunque los términos son negativos, el comportamiento es el mismo: $$ \lim_{n \rightarrow \infty} \frac{1}{-n} = 0 $$

Y si tomamos el valor absoluto, obtenemos una sucesión positiva que también se aproxima a cero:

$$ \lim_{n \rightarrow \infty} \left| \frac{1}{-n} \right| = 0 $$

Por qué esto es importante

El concepto de sucesión infinitesimal es clave en el análisis matemático. Permite describir con precisión cómo se comportan las funciones cuando sus variables crecen sin límite o se aproximan a ciertos valores. Esta idea es la base de nociones como el límite, la continuidad y la derivada.

Una mirada más formal

Podemos definir el valor absoluto de la sucesión a_n como una nueva sucesión b_n:

$$ b_n = |a_n| $$

De acuerdo con la definición rigurosa de límite, una sucesión converge si:

$$ \forall \epsilon > 0, \exists v : |b_n - l| < \epsilon \quad \forall n > v $$

En el caso de una sucesión infinitesimal, el límite es l = 0, de modo que la condición se expresa como:

$$ \forall \epsilon > 0, \exists v : |b_n| < \epsilon \quad \forall n > v $$

Y como |b_n| = |a_n|, concluimos que la convergencia del valor absoluto a cero implica que la propia sucesión es infinitesimal.

Este razonamiento, aunque formal, expresa una idea intuitiva muy potente: cuanto más avanza la sucesión, más se aproxima a cero - y en matemáticas, esa cercanía infinita es lo que realmente cuenta.