Sucesiones de Cauchy
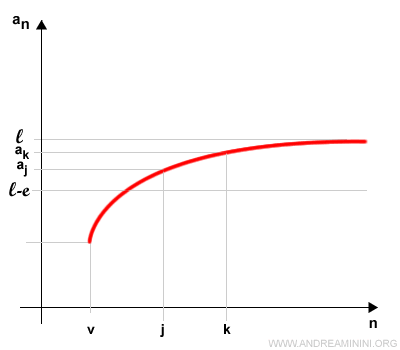
Una sucesión de Cauchy es una sucesión de números reales en la que, a partir de cierto punto, los términos están cada vez más cerca entre sí. En términos formales, para todo ε > 0 existe un índice v tal que $$ | a_k - a_j | < \epsilon $$ siempre que k, j > v.
Este tipo de sucesiones es esencial en el análisis real, ya que permite caracterizar la convergencia sin necesidad de conocer el valor del límite. De hecho, toda sucesión convergente es de Cauchy, y toda sucesión de Cauchy es convergente.
El criterio de Cauchy para la convergencia
Una sucesión converge si, y solo si, es una sucesión de Cauchy.
Por qué toda sucesión convergente es de Cauchy
Toda sucesión convergente cumple automáticamente la condición de Cauchy.
Demostración
Supongamos que la sucesión an converge a un límite finito l. Por definición, para todo ε > 0 existe un índice v tal que, para todo n > v:
$$ |a_n - l| < \frac{\epsilon}{2} $$
Tomemos dos términos cualesquiera de la sucesión, ak y aj, con k, j > v. Se cumple que:
$$ |a_k - l| < \frac{\epsilon}{2}, \qquad |a_j - l| < \frac{\epsilon}{2} $$
Si sumamos ambas desigualdades obtenemos:
$$ |a_k - l| + |a_j - l| < \epsilon $$
Por la desigualdad triangular,
$$ |a_k - a_j| \le |a_k - l| + |l - a_j| < \epsilon $$
Es decir, los términos de la sucesión se aproximan entre sí tanto como queramos: exactamente la condición que define una sucesión de Cauchy.
Por qué toda sucesión de Cauchy es convergente
Si una sucesión es de Cauchy, necesariamente converge.
De este modo, una sucesión es convergente si, y solo si, cumple la condición de Cauchy. Ambas propiedades son equivalentes.
Nota. Si una sucesión an no es de Cauchy, entonces diverge o no tiene límite definido.
Demostración
Toda sucesión de Cauchy está acotada. En efecto, para todo k, j > v:
$$ |a_k - a_j| < 1 $$
Si fijamos j, obtenemos:
$$ a_j - 1 < a_k < a_j + 1 $$
Por tanto, los términos de la sucesión quedan dentro de un intervalo finito, lo que demuestra que está acotada.
Una sucesión acotada, según el teorema de Bolzano-Weierstrass, posee al menos una subsucesión convergente ank. Supongamos que dicha subsucesión converge a l:
$$ \lim_{n_k \rightarrow \infty} a_{n_k} = l $$
Queremos probar que toda la sucesión an converge al mismo límite l.
Tomemos un ε > 0 y consideremos ε/2. Por la condición de Cauchy:
$$ |a_k - a_j| < \frac{\epsilon}{2} \quad \forall j, k > v $$
Además, como la subsucesión es convergente:
$$ |a_{n_k} - l| < \frac{\epsilon}{2} \quad \forall k > v $$
Combinando ambas desigualdades y aplicando la propiedad triangular:
$$ |a_n - l| \le |a_n - a_{n_k}| + |a_{n_k} - l| < \epsilon $$
Por tanto,
$$ |a_n - l| < \epsilon \quad \forall n > k $$
lo que demuestra que la sucesión completa an converge al mismo límite:
$$ \lim_{n \rightarrow \infty} a_n = l $$
Nota. Dado que nk ≥ k y k > v, se cumple que nk > v. En otras palabras, cada índice de la subsucesión también pertenece a la parte "estable" de la sucesión de Cauchy.