Límite de una función compuesta

Sea f(g(x)) una función compuesta. Decimos que $$ \lim_{x \rightarrow x_0} f(g(x)) = l $$ si se verifican las condiciones $$ \lim_{x \rightarrow x_0} g(x) = y_0 $$ y $$ \lim_{y \rightarrow y_0} f(y) = l $$ y, además, existe un δ>0 tal que $$ g(x) \ne y_0 \:\:\: \forall x \ne x_0 \in (x_0-δ, x_0+δ) $$ En otras palabras, el límite de la función compuesta es l cuando la función interior se aproxima a y₀, la función exterior tiende a l cuando su variable se acerca a y₀, y g(x) no toma exactamente el valor y₀ en un entorno perforado de x₀.

Para calcular el límite de una función compuesta cuando x→x₀ , conviene seguir un procedimiento claro en dos pasos:

$$ \lim_{x \to x_0} f(g(x)) $$

Primero, se calcula el límite de la función interior:

$$ \lim_{x \rightarrow x_0} g(x) = y_0 $$

Después, se evalúa el límite de la función exterior en el punto y₀:

$$ \lim_{y \rightarrow y_0} f(y) = l $$

Si este segundo límite existe, entonces se puede afirmar que

$$ \lim_{x \rightarrow x_0} f(g(x)) = l $$

Caso particular. Si la función interior \( g(x) \) es continua en \( x_0 \) y la función exterior \( f(z) \) es continua en \( z_0 = g(x_0) \), entonces la función compuesta \( f(g(x)) \) también es continua en \( x_0 \). En este caso, el límite se obtiene por sustitución directa: \[ \lim_{x \to x_0} f(g(x)) = f(g(x_0)) \] Este resultado resume una idea fundamental del análisis: la continuidad se conserva al componer funciones.

Ejemplo 1

Consideremos la función

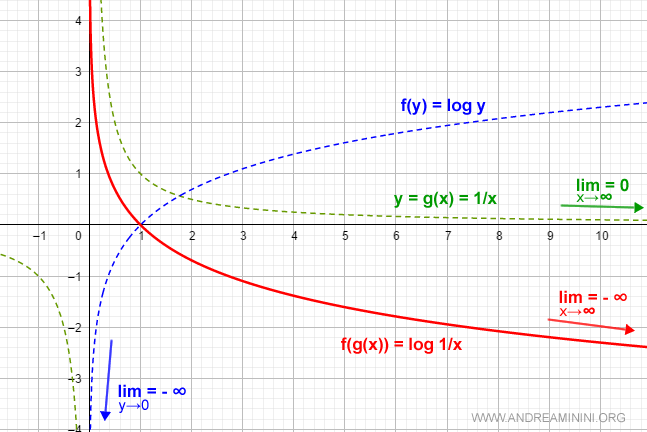
$$ f(x) = \log \frac{1}{x} $$

Puede escribirse como función compuesta f(g(x)), donde

$$ y = g(x) = \frac{1}{x} $$

$$ f(y) = \log y $$

Calculemos

$$ \lim_{x \rightarrow \infty} \log \frac{1}{x} $$

Primero evaluamos el límite interior:

$$ y_0 = \lim_{x \rightarrow \infty} g(x) = \lim_{x \rightarrow \infty} \frac{1}{x} = 0 $$

Después analizamos el límite exterior. Como el logaritmo solo está definido para valores positivos, debemos considerar el límite lateral derecho:

$$ l = \lim_{y \rightarrow 0^+} \log y = -\infty $$

Por lo tanto,

$$ \lim_{x \rightarrow \infty} \log \frac{1}{x} = -\infty $$

Ejemplo 2

Consideremos la función compuesta

$$ f(g(x)) = \sin(4x) $$

La función interior es

$$ z = g(x) = 4x $$

y la función exterior es

$$ f(z) = \sin z $$

Ambas funciones son continuas en \( \mathbb{R} \).

Calculemos

$$ \lim_{x \to \frac{\pi}{4}} \sin(4x) $$

Primero evaluamos el límite interior:

$$ \lim_{x \to \frac{\pi}{4}} 4x = 4 \cdot \frac{\pi}{4} = \pi $$

Como la función seno es continua en \( \pi \), basta sustituir directamente:

$$ \sin(\pi) = 0 $$

En consecuencia,

$$ \lim_{x \to \frac{\pi}{4}} \sin(4x) = 0 $$

Ejemplo 3

Calculemos

$$ \lim_{x \to 2} \sqrt{x^2 + 1} $$

La función interior es

$$ z = g(x) = x^2 + 1 $$

La función exterior es

$$ f(z) = \sqrt{z} $$

Primero evaluamos el límite interior:

$$ \lim_{x \to 2} (x^2 + 1) = 4 + 1 = 5 $$

Como la función raíz cuadrada es continua en \( z = 5 \), sustituimos directamente:

$$ f(5) = \sqrt{5} $$

Por lo tanto,

$$ \lim_{x \to 2} \sqrt{x^2 + 1} = \sqrt{5} $$

Demostración

Supongamos que

$$ \lim_{x \rightarrow x_0} f(g(x)) = l $$

Sea \( \{x_n\} \) una sucesión en el dominio de f(g(x)) tal que

$$ \lim_{n \rightarrow \infty} x_n = x_0 $$

Por la caracterización secuencial del límite, para todo δ>0 existe un índice v tal que

$$ |x_n - x_0| < \delta \:\:\: \forall n > v $$

Definimos la sucesión

$$ y_n = g(x_n) $$

Como

$$ \lim_{x \rightarrow x_0} g(x) = y_0 $$

se sigue que

$$ \lim_{n \rightarrow \infty} y_n = y_0 $$

Además, dado que g(x) no toma el valor y₀ en un entorno perforado de x₀, se cumple que

$$ y_n \ne y_0 \:\:\: \forall n > v $$

Aplicando nuevamente la caracterización secuencial, la hipótesis

$$ \lim_{y \rightarrow y_0} f(y) = l $$

implica que

$$ \lim_{n \rightarrow \infty} f(y_n) = l $$

Por consiguiente,

$$ \lim_{n \rightarrow \infty} f(g(x_n)) = l $$

Con esto queda demostrada la proposición.