Límite por la derecha
Una función f(x), definida en un intervalo (c, d), tiene un límite por la derecha en el punto c si: $$ \lim_{x \rightarrow c^+} f(x) = l. $$ En términos sencillos, esto significa que para cualquier ε > 0, existe un δ > 0 tal que, siempre que $$ c < x < c + δ, \text{ se cumple que } |f(x) - l| < ε. $$
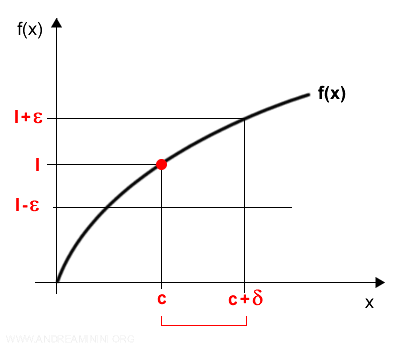
En otras palabras, cuando observamos los valores de x que se acercan a c desde la derecha - es decir, desde valores mayores que c - , si f(x) se aproxima cada vez más a un número l, decimos que la función tiene un límite por la derecha en c.
Nota. Al analizar el límite por la derecha de una función en un punto, solo se consideran los valores de x que se aproximan a c desde la derecha. Los valores a la izquierda de c, o el propio valor de la función en c, no influyen en este tipo de límite y pueden existir o no.
Ejemplo práctico
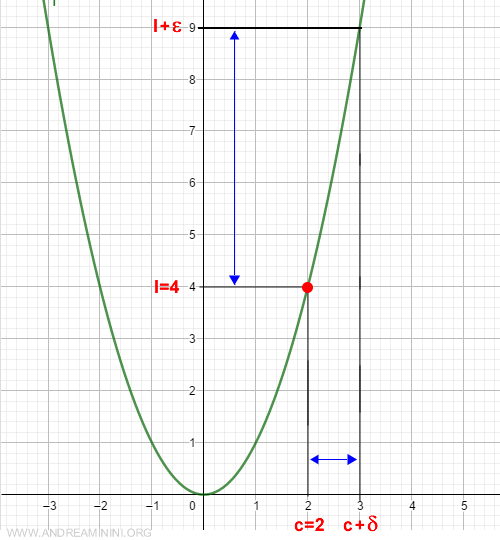
Veamos un ejemplo sencillo con la función f(x) = x2 en el punto c = 2.
El límite por la derecha de la función es:
$$ \lim_{x \rightarrow 2^+} f(x) = 4 $$
Comprobación paso a paso
Supongamos que elegimos un valor arbitrario ε = 5, con ε > 0.
$$ l + ε = 4 + 5 = 9 $$
Podemos escoger δ = 1, también positivo, y definir el intervalo:
$$ (c, c + δ) = (2, 2 + 1) = (2, 3) $$
En cualquier valor de x dentro del intervalo abierto (2, 3), la diferencia entre f(x) y el límite l es menor que ε.
Por tanto, confirmamos que el límite por la derecha de la función f(x) en x = 2 es efectivamente 4.
Límite infinito por la derecha en x₀
Límite por la derecha +∞
Sea f(x) una función definida en un entorno derecho de $ x_0 $ (aunque no necesariamente en $ x_0 $). Decimos que f(x) tiende a +∞ cuando x se aproxima a $ x_0 $ por la derecha, y lo expresamos de la siguiente forma: \[ \lim_{x \to x_0^+} f(x) = +\infty \] si, para todo número real positivo $ M>0 $, es posible determinar un entorno derecho $ I^+(x_0) $ tal que se cumpla: \[ f(x) > M \] para todo $ x $ perteneciente a dicho entorno. De manera formal: \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) > M,\ \forall \ x \in I^+(x_0) \]
En esta situación, también se dice que la función f diverge positivamente por la derecha de $ x_0 $.
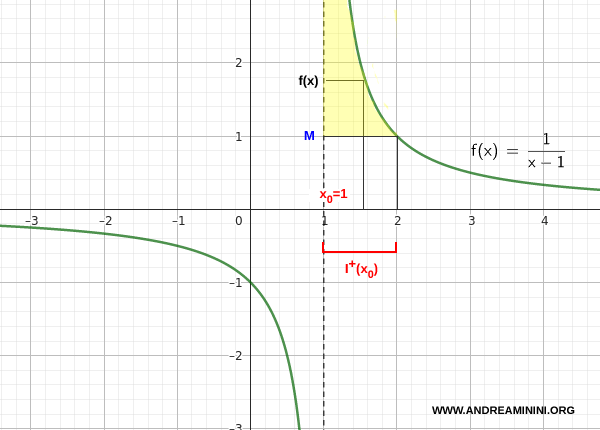
Veamos un ejemplo concreto. Consideremos la función
\[ f(x) = \frac{1}{x - 1} \]
Estudiamos su comportamiento cuando $ x $ se aproxima a 1 por la derecha.
Para valores de $ x > 1 $, el denominador es positivo y se hace cada vez más pequeño, acercándose a cero. Como resultado, los valores de f(x) aumentan sin límite.
Por lo tanto, se obtiene:
\[ \lim_{x \to 1^+} \frac{1}{x - 1} = +\infty \]
En consecuencia, la función diverge positivamente por la derecha de 1.
Límite por la derecha -∞
Decimos que f(x) tiende a -∞ cuando x se aproxima a x₀ por la derecha, y lo escribimos: \[ \lim_{x \to x_0^+} f(x) = -\infty \] si, para todo número real positivo $ M > 0 $, se puede determinar un entorno derecho $ I^+(x_0) $ tal que: \[ f(x) < -M \] para todo $ x $ perteneciente a dicho entorno. De forma simbólica: \[ \forall \ M > 0 \ \exists \ I^+(x_0) \ | \ f(x) < -M,\ \forall \ x \in I^+(x_0) \]
En este caso, se dice que la función f diverge negativamente por la derecha de x₀.
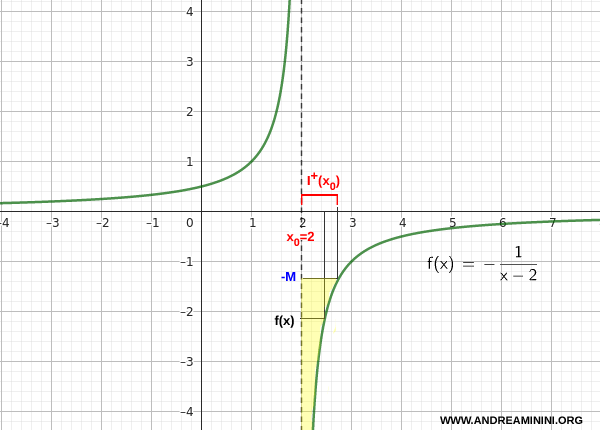
Consideremos ahora la función
\[ f(x) = -\frac{1}{x - 2} \]
Analizamos el límite cuando x se aproxima a 2 por la derecha.
Para $ x > 2 $, el denominador es positivo y tiende a cero. Sin embargo, el signo negativo que precede a la fracción hace que el valor de f(x) sea negativo, con un valor absoluto cada vez mayor.
Por lo tanto:
\[ \lim_{x \to 2^+} \left( -\frac{1}{x - 2} \right) = -\infty \]
En consecuencia, la función diverge negativamente por la derecha de 2.
Y así sucesivamente, este razonamiento puede aplicarse a muchos otros casos similares.