Ángulos Explementarios
Ángulos explementarios son dos ángulos cuyas medidas suman 360 grados, formando así un círculo completo.
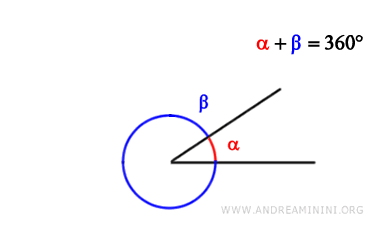
Dicho de otro modo, dos ángulos explementarios completan una vuelta entera alrededor de un círculo.
Un Ejemplo Práctico
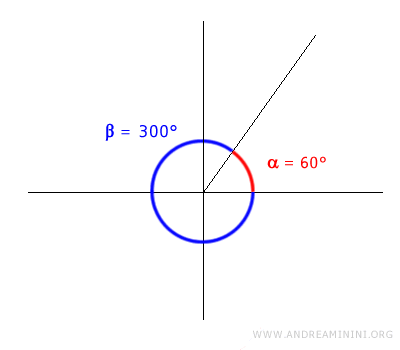
Analicemos el caso de dos ángulos. Uno de ellos, alfa, mide 60°, y el otro, beta, mide 300°.
$$ \alpha = 60° $$
$$ \beta = 300° $$
Si sumamos estos dos ángulos, obtenemos un total de 360 grados.
$$ \alpha + \beta = 60° + 300° = 360° $$
Por lo tanto, estos dos ángulos son explementarios.
Otro ejemplo podría ser un ángulo recto de 90 grados y un ángulo de 270 grados. En este caso, la suma de sus medidas es 360 grados, lo que los convierte en ángulos explementarios. $$ 90° + 270° = 360° $$ De igual forma, cualquier par de ángulos cuya suma forme un círculo completo se considera explementario. $$ \alpha + \beta = 360° $$
Notas
Algunas consideraciones adicionales sobre los ángulos explementarios:
- La definición de ángulos explementarios solo tiene sentido aplicada a pares de ángulos. Por ello, un único ángulo no puede considerarse «explementario» de manera aislada.
- Los ángulos explementarios forman parte del grupo de ángulos relacionados por la suma de sus medidas, junto con los ángulos complementarios (suma de 90°) y suplementarios (suma de 180°).
- Dado cualquier ángulo alfa, es posible hallar el ángulo beta que forme con él un par explementario restándole su medida a 360°: $$ \beta = 360° - \alpha $$ Por ejemplo, si el ángulo alfa mide 120°, el otro ángulo del par explementario será de 240°: $$ \beta = 360° - 120° = 240° $$
- Si un ángulo cóncavo y uno convexo comparten los mismos lados y vértice, constituyen un par de ángulos explementarios.
Y así sucesivamente.