El lado de un hexágono es igual al radio de su circunferencia circunscrita
La longitud del lado de un hexágono regular coincide exactamente con el radio del círculo que lo circunscribe.
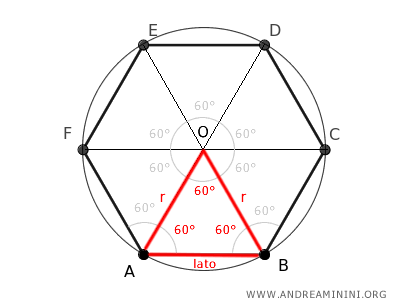
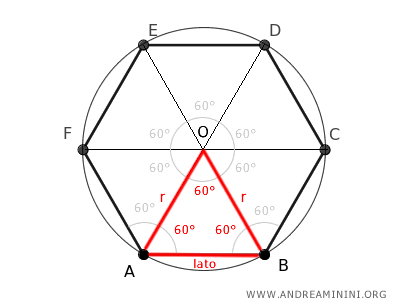
Esto ocurre porque un hexágono regular se puede descomponer en seis triángulos equiláteros congruentes.
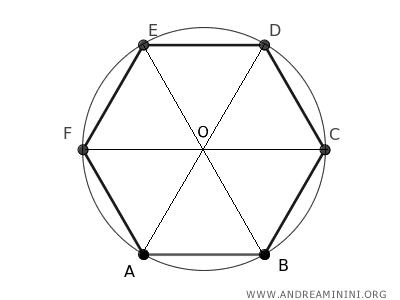
Cada uno de estos triángulos tiene como base uno de los lados del hexágono, mientras que sus otros dos lados son radios que parten del centro del hexágono - que es también el centro de la circunferencia circunscrita - y llegan hasta los vértices.
Estos triángulos son equiláteros, ya que todos sus lados y ángulos tienen la misma medida.
El ángulo completo de 360° que hay en el centro O se divide en seis partes iguales, generando seis ángulos de 60°.
Por tanto, el ángulo opuesto a la base de cada triángulo mide 60°.
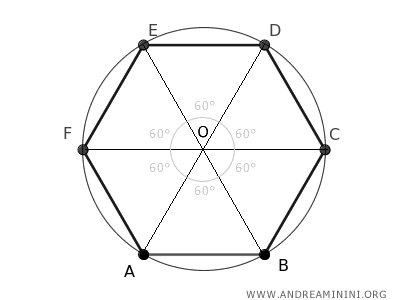
Dado que cada ángulo interior de un hexágono regular mide 120°, los ángulos adyacentes a la base de los triángulos también resultan ser de 60°.
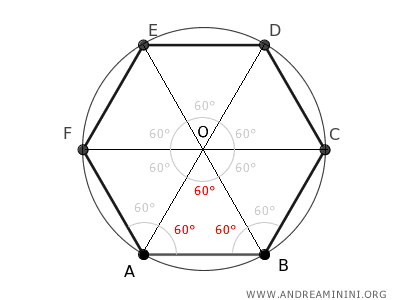
Esto demuestra que todos los triángulos que conforman el hexágono son triángulos equiláteros, ya que cada uno de sus ángulos mide 60°.
La base de cada triángulo coincide con un lado del hexágono, mientras que los otros dos lados corresponden a los radios de la circunferencia.
Y como en un triángulo equilátero todos sus lados son iguales, se concluye que el radio (que constituye uno de esos lados) es exactamente igual a la longitud del lado del hexágono.
Esta propiedad de los hexágonos regulares los hace especialmente útiles tanto en demostraciones geométricas como en numerosas aplicaciones prácticas.
Y así sucesivamente.