Lado de un hexágono y radio de su circunferencia inscrita
La longitud del lado (l) de un hexágono regular se relaciona con el radio (r) de su circunferencia inscrita mediante la siguiente fórmula: $$ l = \frac{2 \sqrt{3}}{3} \cdot r $$ 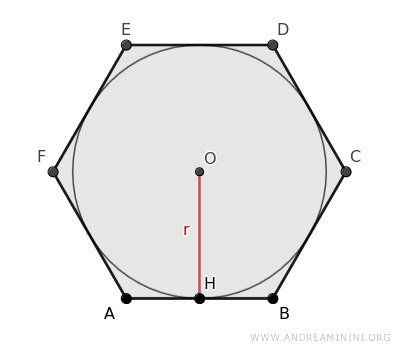
El radio de la circunferencia inscrita, que coincide con la apotema del hexágono, guarda exactamente esta misma relación con la longitud del lado (a) del hexágono.
$$ l = \frac{2 \sqrt{3}}{3} \cdot a $$
Esta última expresión es la más habitual, aunque en esencia es idéntica a la anterior.
Fórmulas inversas. De forma análoga, se puede calcular el radio (r) de la circunferencia inscrita a partir de la longitud del lado (l) del hexágono usando la fórmula inversa: $$ r = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$ o, en el caso de la apotema: $$ a = l \cdot \frac{3}{2 \sqrt{3}} = l \cdot \frac{\sqrt{3} }{2} $$
Un ejemplo práctico
Imaginemos un hexágono regular cuyos lados miden 2 y cuya circunferencia inscrita tiene un radio r = 1.7321.
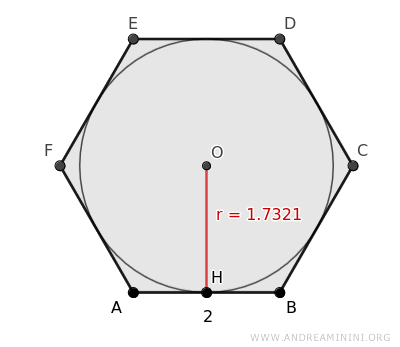
Podemos utilizar la fórmula para calcular la longitud del lado a partir del radio de la circunferencia inscrita:
$$ l = \frac{2 \sqrt{3}}{3} \cdot r $$
En este caso, el radio es r = 1.7321
$$ l = \frac{2 \sqrt{3}}{3} \cdot 1.7321 $$
Realizando los cálculos, obtenemos que la longitud exacta del lado del hexágono es:
$$ l = 2 $$
Aquí, el radio (r) coincide también con la apotema (a) del hexágono.
La demostración
Consideremos un hexágono regular con una circunferencia inscrita centrada en O y de radio r.
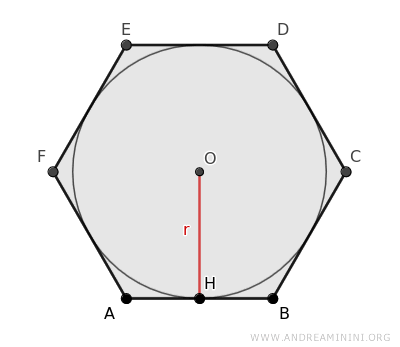
El centro de la circunferencia inscrita coincide con el centro del hexágono regular, ya que es el punto donde se cortan sus diagonales.
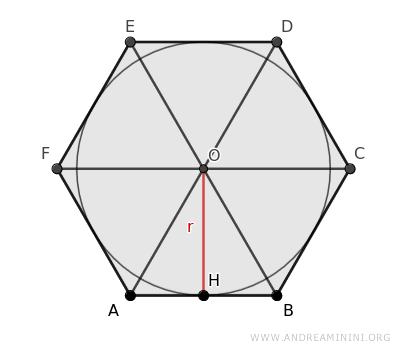
Las diagonales dividen el hexágono en seis triángulos, cada uno de los cuales divide el ángulo central en seis partes iguales de 360°/6 = 60°.
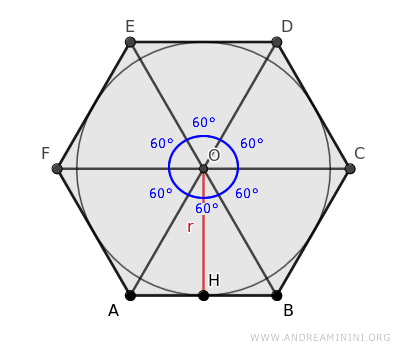
Estos triángulos son congruentes porque, según los criterios de congruencia de triángulos, poseen dos lados iguales y el ángulo comprendido también es congruente (60°).
Gracias a esta simetría, basta con analizar uno solo de estos triángulos, por ejemplo el triángulo ABO.
Las diagonales dividen los ángulos interiores del hexágono (de 120°) en dos ángulos congruentes de 60° cada uno.
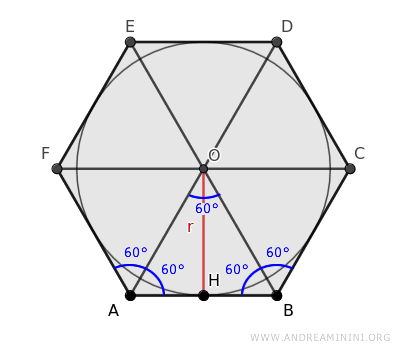
Esto implica que el triángulo ABO tiene sus tres ángulos de 60° y, por tanto, es un triángulo equilátero.
Ahora queremos establecer la relación entre el radio (r) de la circunferencia inscrita y la longitud del lado (l) del hexágono.
El radio r divide el triángulo equilátero ABO en dos triángulos rectángulos: AHO y BHO.
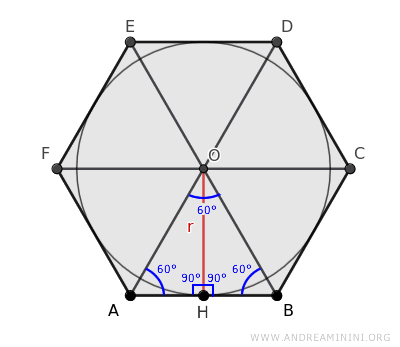
Podemos aplicar el teorema de Pitágoras a uno de estos triángulos rectángulos para calcular la longitud del cateto OH (es decir, el radio r).
Por ejemplo, apliquemos el teorema de Pitágoras al triángulo AHO:
$$ \overline{OH} = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$
El segmento OH corresponde al radio r de la circunferencia inscrita:
$$ r = \sqrt{\overline{AO}^2 - \overline{AH}^2} $$
El segmento AO es congruente con el lado del hexágono (l), ya que el triángulo ABO es equilátero.
$$ r = \sqrt{l^2 - \overline{AH}^2} $$
El segmento AH mide la mitad del lado del hexágono, es decir, l/2.
$$ r = \sqrt{l^2 - \left( \frac{l}{2} \right)^2} $$
Desarrollamos la expresión algebraicamente:
$$ r = \sqrt{l^2 - \frac{l^2}{4} } $$
$$ r = \sqrt{ \frac{4l^2 - l^2}{4} } $$
$$ r = \sqrt{ \frac{3l^2}{4} } $$
$$ r = \frac{l}{2} \sqrt{3} $$
A partir de aquí, despejamos l:
$$ r \cdot \frac{2}{\sqrt{3}} = \frac{l}{2} \sqrt{3} \cdot \frac{2}{\sqrt{3}} $$
$$ r \cdot \frac{2}{\sqrt{3}} = l $$
Para eliminar la raíz del denominador, multiplicamos y dividimos la fracción de la izquierda por la raíz de tres:
$$ r \cdot \frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = l $$
$$ r \cdot \frac{2 \sqrt{3}}{ \sqrt{3} \cdot \sqrt{3} } = l $$
$$ r \cdot \frac{2 \sqrt{3}}{ \sqrt{3 \cdot 3} } = l $$
$$ r \cdot \frac{2 \sqrt{3}}{ \sqrt{3^2} } = l $$
$$ r \cdot \frac{2 \sqrt{3}}{3} = l $$
Finalmente, reordenamos términos:
$$ l = \frac{2 \sqrt{3}}{3} \cdot r $$
Así queda demostrada la fórmula que relaciona el radio (r) de la circunferencia inscrita con la longitud del lado (l) de un hexágono regular.
Nota. Como el radio de la circunferencia inscrita coincide con la apotema de un hexágono regular (r = a), también podemos expresar la fórmula de forma equivalente así: $$ l = \frac{2 \sqrt{3}}{3} \cdot a $$
Y así sucesivamente.