Cómo Hallar el Punto Medio de un Segmento de Recta
Para determinar el punto medio de un segmento de recta AB, coloca el compás en el extremo A y ábrelo con una amplitud mayor a la mitad de la longitud del segmento. Traza un arco.
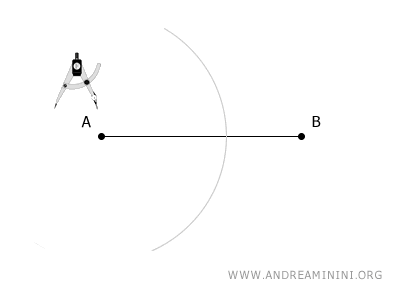
A continuación, sitúa el compás en el extremo B y dibuja un segundo arco con la misma apertura que utilizaste en el primer arco.
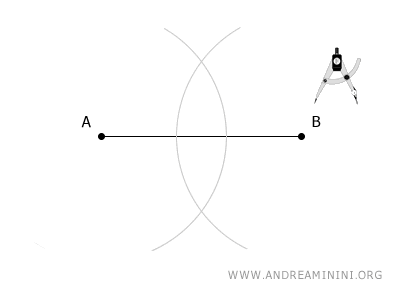
Estos dos arcos se intersecan en los puntos C y D.
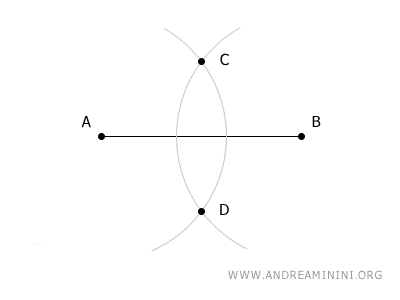
El segmento de recta que une los puntos C y D corta al segmento AB exactamente en su punto medio, denominado M.
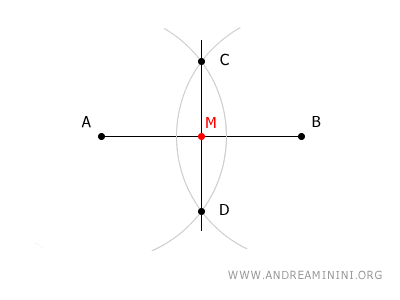
De esta manera, se obtiene el punto medio del segmento.
Demostración. Por construcción, los segmentos $ AC \cong BC \cong AD \cong BD $ son congruentes. Esto implica de forma directa que los triángulos $ ACD $ y $ BCD $ son congruentes según el tercer criterio de congruencia de triángulos, ya que tienen tres pares de lados correspondientes congruentes.

Como consecuencia, los ángulos correspondientes de los triángulos $ \triangle ACD $ y $ \triangle BCD $ también son congruentes. En particular, lo relevante aquí es que $ \angle ACD \cong \angle BCD $, lo que indica que el segmento $ CM $ es la bisectriz del ángulo $ \angle ACB $ en el triángulo $ ABC $. Dado que $ \triangle ABC $ es un triángulo isósceles (donde $ AC \cong BC $), este dato resulta fundamental.

En cualquier triángulo isósceles, la bisectriz del ángulo en el vértice coincide también con la mediana. Y como la mediana, por definición, divide el lado opuesto en dos partes iguales, esto demuestra que $ M $ es efectivamente el punto medio del segmento $ AB $.
Y eso es todo.