Diferencia de Segmentos

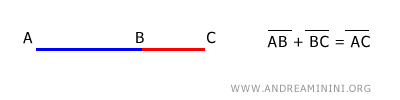
La diferencia entre dos segmentos AC y AB es un nuevo segmento BC, tal que, al sumar BC y AB, se obtiene una longitud igual a la de AC. $$ AC - AB = BC \Longleftrightarrow AB + BC = AC $$

Por ejemplo, si el segmento AC mide 7 unidades y el segmento AB mide 5 unidades:

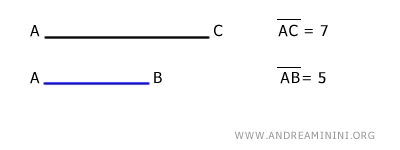
La “resta” del segmento AB al segmento AC equivale a la diferencia de sus longitudes:

$$ AC - AB = 7 - 5 = 2 $$

Por lo tanto, el segmento resultante BC = AC - AB tiene una longitud de 2 unidades.

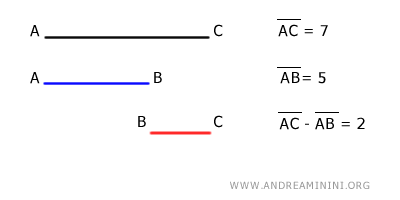
En efecto, al sumar AB y BC, se obtiene la longitud de AC:

$$ AB + BC \cong AC $$

Nota. Partiendo de la suma AB+BC: $$ AB + BC $$ Sabemos que BC es la diferencia entre AC y AB, es decir, BC=AC-AB: $$ AB + BC \cong AB + (AC - AB ) $$ El resultado final es la longitud del segmento AC: $$ AB + BC \cong AB + (AC - AB ) \cong AC $$

Así, la suma AB+BC es congruente con AC.

Nota. En geometría, cuando hablamos de restar segmentos, nos referimos a restar sus longitudes, y no los segmentos en sí mismos. La geometría se ocupa de magnitudes como longitudes, ángulos, áreas y volúmenes, más que de números puros. Por ello, cualquier operación matemática (suma, resta, multiplicación, etc.) aplicada a objetos geométricos se refiere siempre a sus medidas (longitudes, áreas, volúmenes, ángulos, etc.) y no a los objetos geométricos en forma abstracta.

Observaciones

Algunas observaciones sobre la diferencia entre segmentos:

• Si la diferencia entre las longitudes de dos segmentos AC y AB es cero, entonces los segmentos AC y AB son congruentes, es decir, tienen exactamente la misma longitud. $$ AC - AB = 0 \ \ \Longrightarrow \ \ AC \cong AB $$

  Ejemplo
  
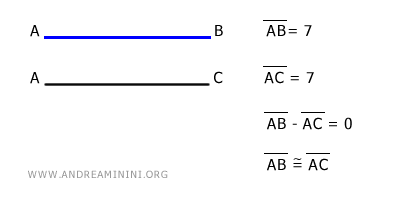
  Por el contrario, si la diferencia entre AB y AC no es cero, los segmentos no son congruentes, lo que implica que tienen longitudes distintas. En ese caso, uno será mayor y el otro menor.

• Si la diferencia AC-AB es positiva, entonces la longitud del segmento AC es mayor que la de AB. $$ AC - AB > 0 \ \ \Longrightarrow \ \ AC > AB $$

  Ejemplo
  

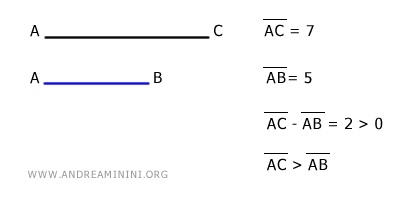
• Si la diferencia AB-AC es negativa, significa que la longitud del segmento AB es menor que la del segmento AC. $$ AB - AC < 0 \ \ \Longrightarrow \ \ AB < AC $$

  Ejemplo
  

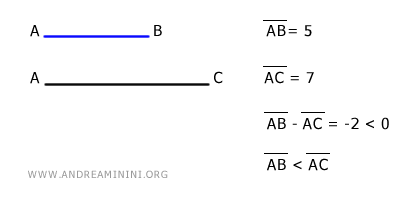
• Si AB ≅ CD y EF ≅ GH (siendo AB > EF), entonces AB - EF ≅ CD - GH, es decir, las diferencias entre dos pares de segmentos congruentes también son congruentes. $$ AB \cong CD \ , \ EF \cong GH \ | \ AB > EF \ \Longrightarrow AB - EF \cong CD - GH $$

  Ejemplo
  

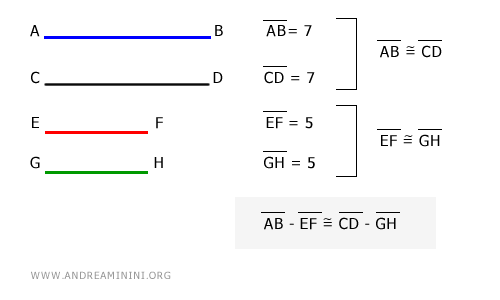
Y así sucesivamente.