Bisectriz de un Segmento
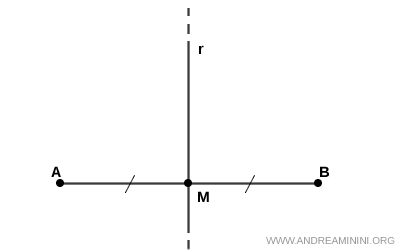
La bisectriz de un segmento, también llamada mediatriz, es la recta perpendicular al segmento que pasa por su punto medio.

La bisectriz de un segmento constituye un lugar geométrico, ya que todos los puntos que se hallan sobre ella se encuentran a la misma distancia de los extremos del segmento.
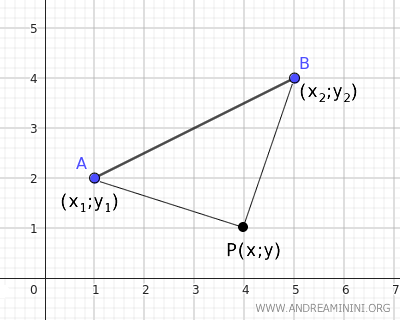
Por ejemplo, consideremos el segmento AB:

El punto M es el punto medio del segmento AB, ya que lo divide en dos partes congruentes, AM y MB.

La bisectriz del segmento AB es la recta r, que pasa por el punto medio M y es perpendicular al segmento, formando un ángulo recto de 90°.

Cómo Hallar la Ecuación de la Bisectriz de un Segmento
Para determinar la ecuación de la bisectriz del segmento AB, es necesario encontrar los puntos del plano P(x;y) que se encuentren a la misma distancia de los extremos A(x1;y1) y B(x2;y2) del segmento AB.
$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $

Ejemplo
Consideremos un segmento cuyos extremos son A(1;2) y B(5;4).

Para hallar la ecuación de su bisectriz, debemos determinar los puntos del plano P(x;y) que sean equidistantes de los extremos A(1;2) y B(5;4) del segmento AB.
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
Sustituimos las coordenadas del punto A(1;2) en la ecuación, es decir, x1=1 y y1=2.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Luego sustituimos las coordenadas del punto B(5;4), es decir, x2=5 y y2=4.
$$ \sqrt{(y-2)^2 + (x-1)^2 } = \sqrt{(y-4)^2 + (x-5)^2} $$
Como ambos lados de la ecuación son positivos, podemos elevarlos al cuadrado para eliminar las raíces.
$$ \left( \sqrt{(y-2)^2 + (x-1)^2 } \right)^2 = \left( \sqrt{(y-4)^2 + (x-5)^2} \right)^2 $$
$$ (y-2)^2 + (x-1)^2 = (y-4)^2 + (x-5)^2 $$
Desarrollamos los binomios.
$$ y^2 -4y+4 + x^2-2x+1 = y^2-8y+16 + x^2-10x+25 $$
Eliminamos los términos y2 y x2 en ambos lados de la ecuación.
$$ \require{cancel} \cancel{y^2} -4y+4 + \cancel{x^2}-2x+1 = \cancel{y^2}-8y+16 + \cancel{x^2}-10x+25 $$
Reorganizamos y simplificamos los términos semejantes.
$$ -2x -4y+5 = -10x-8y+41 $$
$$ -2x -4y+5 + 10x + 8y -41 = 0 $$
$$ 8x +4y-36 = 0 $$
Dividimos toda la ecuación entre cuatro para simplificar los coeficientes.
$$ \frac{8x +4y-36}{4} = \frac{0}{2} $$
$$ 2x + y - 9 = 0 $$
Así obtenemos la ecuación de la recta que representa todos los puntos del plano equidistantes de los extremos A y B del segmento AB, es decir, la ecuación de la bisectriz del segmento AB.

La recta obtenida pasa por el punto medio del segmento AB y es perpendicular a este.
Demostración
Consideremos el segmento AB, cuyos extremos son A(x1;y1) y B(x2;y2). Queremos hallar la ecuación de su bisectriz.
La bisectriz de un segmento es un lugar geométrico formado por todos los puntos del plano P(x;y) que se encuentran a la misma distancia de los extremos A y B del segmento AB.
Para determinar estos puntos, calculamos la distancia de un punto genérico P(x;y) a los extremos A(x1;y1) y B(x2;y2) del segmento AB.
- Distancia del punto P al extremo A del segmento
El segmento PA representa la distancia entre P y el punto A, que se determina aplicando el teorema de Pitágoras en el triángulo rectángulo ACP.

En este caso, PA es la hipotenusa del triángulo rectángulo ACP. Sabiendo que CP=|x-x1| y AC=|y-y1| $$ \overline{AP} = \sqrt{ \overline{AC}^2 + \overline{CP}^2} = \sqrt{(y-y_1)^2 + (x-x_1)^2} $$ - Distancia del punto P al extremo B del segmento
El segmento PB mide la distancia entre P y el punto B, y se calcula también mediante el teorema de Pitágoras en el triángulo rectángulo BDP.

Aquí, PB es la hipotenusa del triángulo rectángulo BDP. Sabiendo que DP=|x-x2| y BD=|y-y2| $$ \overline{BP} = \sqrt{ \overline{BD}^2 + \overline{DP}^2} = \sqrt{(y-y_2)^2 + (x-x_2)^2} $$
Una vez calculadas las distancias desde el punto P hasta los extremos A y B, que corresponden a las longitudes de los segmentos AP y BP, las igualamos entre sí:
$$ \overline{AP} = \overline{BP} $$
$$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2 } }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$
Esta ecuación permite deducir la ecuación de la bisectriz del segmento, conociendo las coordenadas de sus extremos A(x1;y1) y B(x2;y2).
Método Alternativo para Hallar la Ecuación de la Bisectriz de un Segmento
Para determinar la bisectriz de un segmento, podemos considerarla como la recta que pasa por el punto medio del segmento y forma con él un ángulo recto de 90°.
Ejemplo
Consideremos el mismo segmento del ejemplo anterior, cuyos extremos son A(1;2) y B(5;4).

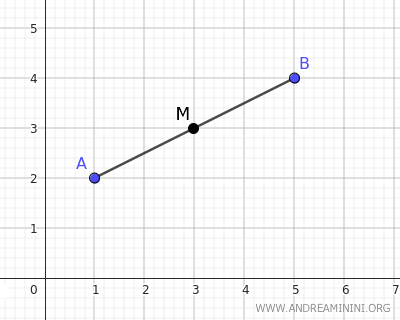
En primer lugar, calculamos el punto medio del segmento promediando las coordenadas x e y de los extremos A(1;2) y B(5;4).
$$ x_M = \frac{x_A+x_B}{2} = \frac{1+5}{2} = \frac{6}{2} = 3 $$
$$ y_M = \frac{y_A+y_B}{2} = \frac{2+4}{2} = \frac{6}{2} = 3 $$
Por lo tanto, el punto medio del segmento AB se encuentra en las coordenadas (xM; yM) = (3; 3).
A continuación, hallamos la ecuación de la recta que contiene al segmento AB.
La ecuación de la recta que pasa por dos puntos en el plano A(x1; y1) y B(x2; y2) es:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
Sustituyamos las coordenadas de los puntos A(1;2) y B(5;4): x1=1, y1=2, x2=5, y2=4.
$$ \frac{y - 2}{4 - 2} = \frac{x - 1}{5 - 1} $$
$$ \frac{y - 2}{2} = \frac{x - 1}{4} $$
$$ 4 \cdot (y - 2) = 2 \cdot (x - 1) $$
Simplificamos dividiendo ambos lados entre dos.
$$ \frac{4 \cdot (y - 2)}{2} = \frac{2 \cdot (x - 1)}{2} $$
$$ 2 \cdot (y - 2) = x - 1 $$
$$ 2y - 4 = x - 1 $$
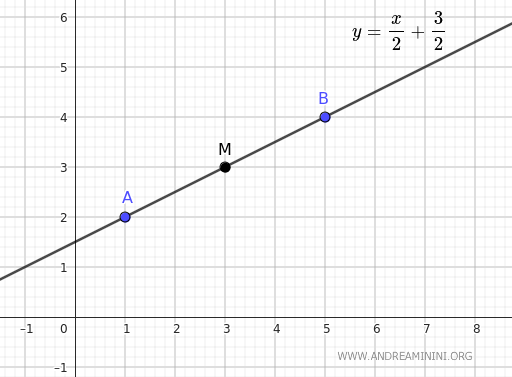
Despejamos y para obtener la ecuación de la recta que contiene al segmento AB:
$$ 2y = x - 1 + 4 $$
$$ y = \frac{x + 3}{2} $$
$$ y = \frac{x}{2} + \frac{3}{2} $$
Por lo tanto, la recta que pasa por los puntos A y B tiene por ecuación y = x/2 + 3/2.
De la ecuación de la recta y = x/2 + 3/2 en forma explícita, obtenemos directamente la pendiente m de la recta, que es m = 1/2.
$$ m = \frac{1}{2} $$
Ahora necesitamos encontrar la ecuación de la recta perpendicular, es decir, aquella que forma un ángulo de 90° con la recta inicial.
$$ y' = m'x + c' $$
Según la condición de perpendicularidad, el producto de las pendientes m y m' de dos rectas perpendiculares es siempre igual a -1.
$$ m \cdot m' = -1 $$
Sustituimos la pendiente m = 1/2 de la recta que contiene al segmento AB.
$$ \frac{1}{2} \cdot m' = -1 $$
De donde se deduce que la pendiente de la recta perpendicular es m' = -2.
$$ m' = -2 $$
Por lo tanto, la ecuación de la recta perpendicular tendrá pendiente m' = -2.
$$ y' = m'x + c' $$
$$ y' = -2x + c' $$
Para hallar la ordenada al origen c', sustituimos las coordenadas del punto medio M(3;3) del segmento AB: x' = 3 y y' = 3.
$$ 3 = -2 \cdot 3 + c' $$
$$ 3 = -6 + c' $$
$$ c' = 9 $$
Una vez obtenida la ordenada al origen c' = 9, la incorporamos en la ecuación de la recta perpendicular.
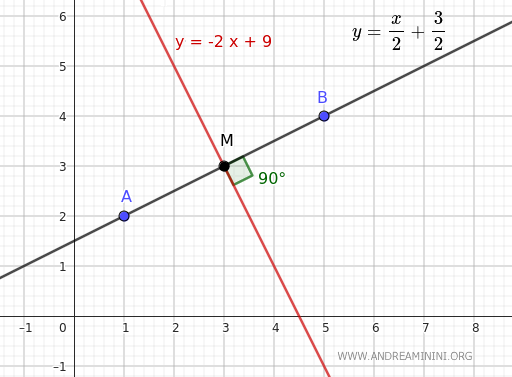
$$ y' = -2x + c' $$
$$ y' = -2x + 9 $$
Así, obtenemos la ecuación de la recta perpendicular al segmento AB que pasa por su punto medio M, es decir, la ecuación de la bisectriz del segmento AB.
Observaciones
Algunas observaciones y aclaraciones:
- Puntos simétricos respecto a un eje
Dados dos puntos A y B que determinan el segmento AB, si una recta r es la bisectriz perpendicular de dicho segmento, entonces A y B son puntos simétricos respecto a la recta r.
- Los puntos sobre la bisectriz están equidistantes de los extremos del segmento
La bisectriz constituye un lugar geométrico, pues todos sus puntos se encuentran a la misma distancia de los extremos A y B del segmento.Demostración: Consideremos un punto P situado sobre la bisectriz r del segmento AB. Queremos demostrar que P está a igual distancia de los extremos A y B. Como r es la bisectriz del segmento AB, se deduce que el punto de intersección M es el punto medio de AB, y por tanto, los segmentos AM y MB son congruentes (AM ≅ MB). En consecuencia, según el primer criterio de congruencia de triángulos (LAL), los triángulos rectángulos AMP y BMP son congruentes, ya que comparten el lado MP, tienen un lado congruente (AM ≅ MB) y el ángulo comprendido es recto (90°). Al ser congruentes, sus lados correspondientes son iguales, y en particular, los segmentos AP ≅ BP son también congruentes.

Demostración recíproca: También puede demostrarse la proposición inversa. Si un punto P es equidistante de los extremos A y B, necesariamente pertenece a la bisectriz r. En este caso, la hipótesis inicial es que P está a igual distancia de A y B (es decir, AP ≅ BP) y que la recta r es la bisectriz del segmento AB. Para demostrar que P pertenece a la recta r, basta observar que el triángulo ABP es un triángulo isósceles, ya que tiene dos lados congruentes (AP ≅ BP). En un triángulo isósceles, la altura coincide con la mediana, por lo que P pertenece necesariamente a la bisectriz r, que es la recta perpendicular al segmento AB que pasa por su punto medio M.
Y así sucesivamente.