Axioma de Transporte de Segmentos
El Axioma de Transporte de Segmentos, también conocido como Postulado de Transporte de Segmentos, es un principio fundamental de la geometría que establece lo siguiente:
Dado un rayo que parte de un punto O y un segmento AB, existe un único punto P sobre el rayo tal que los segmentos AB y OP son congruentes entre sí: $$ AB \cong OP $$
En esencia, este axioma garantiza que siempre es posible trasladar un segmento a lo largo de un rayo o de una recta sin alterar su longitud ni su dirección.
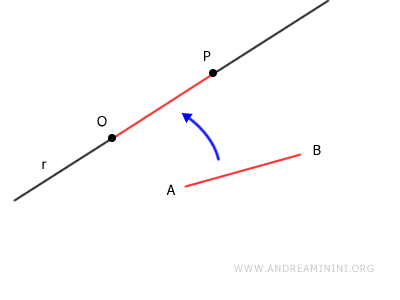
En otras palabras, si desplazamos un segmento AB a lo largo de una recta r, el segmento resultante mantiene exactamente la misma longitud y orientación que el segmento original.
El Axioma de Transporte de Segmentos constituye uno de los cinco postulados fundamentales de la geometría euclidiana.
Nota: Los demás postulados incluyen el postulado de la recta, el postulado de existencia y unicidad de segmentos, el postulado de construcción de ángulos y el postulado de las paralelas.
Este axioma es la base sobre la que se sustentan numerosos teoremas y demostraciones en geometría euclidiana.
Demostración
Consideremos una recta cualquiera y un segmento AB.
Fijamos un punto O sobre la recta, que servirá como origen.
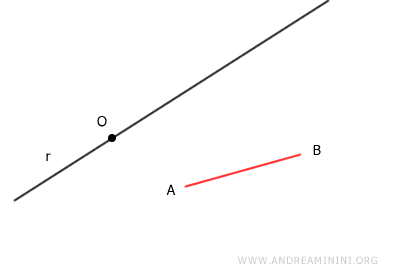
Con ayuda de un compás, trazamos un arco de radio igual a la longitud del segmento AB, centrado en el punto A.
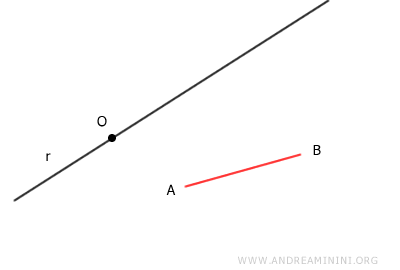
Con la misma abertura del compás, trasladamos ese radio y trazamos un arco sobre la recta, esta vez con centro en el punto O.
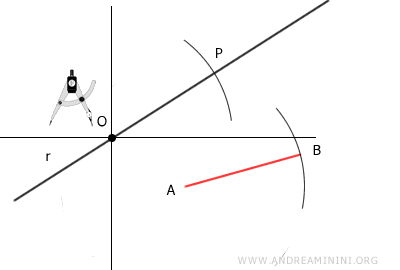
Así determinamos un punto P sobre la recta.
El segmento OP resulta congruente con el segmento AB, ya que ambos tienen la misma longitud, es decir, pertenecen a la misma clase de congruencia.
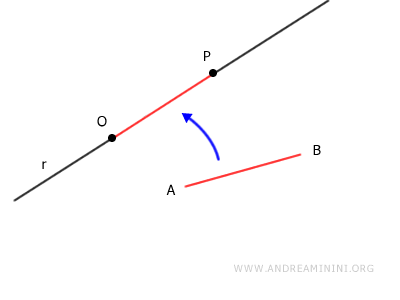
Por tanto, queda demostrado que, una vez fijado el punto O sobre la recta, existe un único punto P que determina un segmento OP congruente con el segmento AB.
Y así sucesivamente.