Ángulos Asociados: α y 3π/2 + α en Trigonometría
En trigonometría, los ángulos alfa (α) y 3π/2 + α se conocen como ángulos asociados y cumplen las siguientes fórmulas de transformación: $$ \sin\left( \frac{3 \pi}{2} + \alpha \right) = - \cos(\alpha) $$ $$ \cos\left( \frac{3 \pi}{2} + \alpha \right) = \sin(\alpha) $$ $$ \tan\left( \frac{3 \pi}{2} + \alpha \right) = - \cot(\alpha) $$ $$ \cot\left( \frac{3 \pi}{2} + \alpha \right) = - \tan(\alpha) $$
Los ángulos α y 3π/2 + α (270° + α) son ángulos asociados, lo que significa que presentan los mismos valores absolutos en las funciones seno, coseno, tangente y cotangente, aunque pueden diferir en el signo.
Demostración y explicación
Analicemos el ángulo α y el ángulo 3π/2 + α en la circunferencia unitaria.
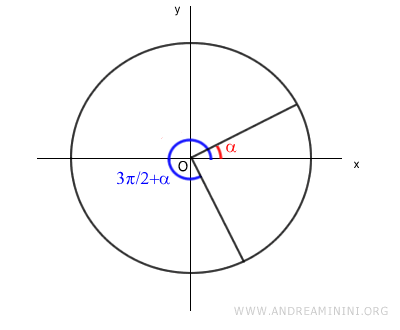
La diferencia entre ambos ángulos es de 270°, es decir, 3π/2 radianes.
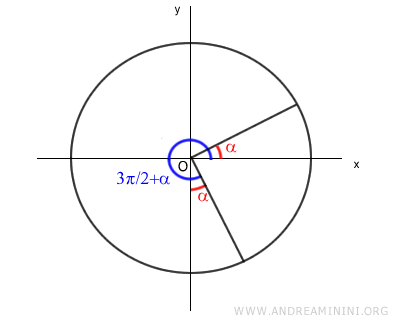
Por este motivo, los triángulos rectángulos OAB y OCD son congruentes, ya que comparten el mismo ángulo agudo (α) y poseen la misma longitud de hipotenusa (OA = OC).
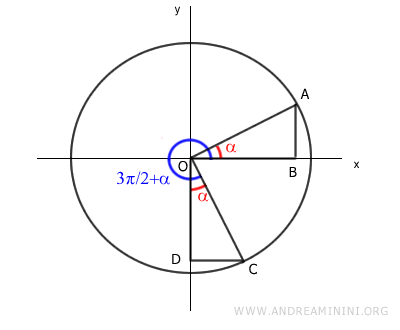
Al ser congruentes, ambos triángulos tienen ángulos idénticos y lados correspondientes de igual longitud.
El segmento OB es igual al segmento OD.
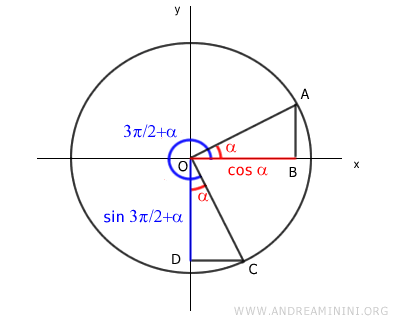
El segmento OB representa el coseno de α sobre el eje x positivo, mientras que el segmento OD corresponde al seno de 3π/2 + α sobre el eje y negativo.
$$ - \sin\left( \frac{3 \pi}{2} + \alpha \right) = \cos \alpha $$
Multiplicando ambos lados de la ecuación por -1, se obtiene:
$$ (-1) \cdot \left( - \sin\left( \frac{3 \pi}{2} + \alpha \right) \right) = (-1) \cdot \cos \alpha $$
$$ \sin\left( \frac{3 \pi}{2} + \alpha \right) = - \cos \alpha $$
Por lo tanto, el seno de 3π/2 + α es igual al opuesto del coseno de α.
Del mismo modo, el segmento AB es igual al segmento CD.
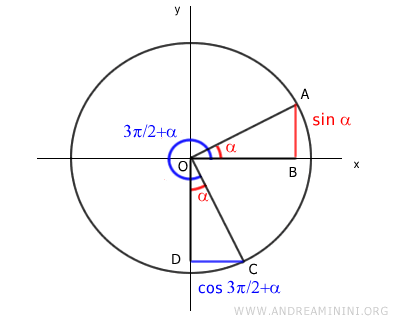
El segmento AB representa el seno de α, mientras que el segmento CD corresponde al coseno de 3π/2 + α.
Por lo tanto, el coseno de 3π/2 + α es igual al seno de α:
$$ \cos\left( \frac{3 \pi}{2} + \alpha \right) = \sin \alpha $$
Una vez establecidas las fórmulas de transformación para seno y coseno, podemos deducir las correspondientes fórmulas para tangente y cotangente.
La tangente se define como el cociente entre el seno y el coseno:
$$ \tan\left( \frac{3 \pi}{2} + \alpha \right) = \frac{ \sin\left( \frac{3 \pi}{2} + \alpha \right) }{ \cos\left( \frac{3 \pi}{2} + \alpha \right) } $$
Como sen(3π/2 + α) = -cos(α) y cos(3π/2 + α) = sen(α), tenemos:
$$ \tan\left( \frac{3 \pi}{2} + \alpha \right) = \frac{ - \cos \alpha }{ \sin \alpha } = - \cot \alpha $$
Por lo tanto, la tangente del ángulo 3π/2 + α es igual al opuesto de la cotangente de α.
La cotangente se define como el cociente entre el coseno y el seno:
$$ \cot\left( \frac{3 \pi}{2} + \alpha \right) = \frac{ \cos\left( \frac{3 \pi}{2} + \alpha \right) }{ \sin\left( \frac{3 \pi}{2} + \alpha \right) } $$
Sabiendo que sen(3π/2 + α) = -cos(α) y cos(3π/2 + α) = sen(α), se deduce que:
$$ \cot\left( \frac{3 \pi}{2} + \alpha \right) = \frac{ \sin \alpha }{ - \cos \alpha } = - \tan \alpha $$
Por lo tanto, la cotangente de 3π/2 + α es igual al opuesto de la tangente de α.
Ejemplo práctico
Calculemos el seno de 330°:
$$ \sin 330° $$
Podemos expresarlo como la suma de 270° + 60°:
$$ \sin\left( 270° + 60° \right) $$
En radianes, se escribe así:
$$ \sin\left( \frac{3 \pi}{2} + \frac{\pi}{3} \right) $$
Los ángulos 3π/2 + α y α son ángulos asociados, donde α = π/3 (es decir, 60°).
$$ \sin\left( \frac{3 \pi}{2} + \alpha \right) = - \cos(\alpha) $$
$$ \sin\left( \frac{3 \pi}{2} + \frac{\pi}{3} \right) = - \cos\left( \frac{\pi}{3} \right) $$
Por lo tanto, el seno de 330° es igual al opuesto del coseno de 60°.
Dado que el coseno de 60° es 1/2, su opuesto es -1/2:
$$ \sin\left( \frac{3 \pi}{2} + \frac{\pi}{3} \right) = - \cos\left( \frac{\pi}{3} \right) = - \frac{1}{2} $$
Por lo tanto, el seno de 330° es -1/2:
$$ \sin 330° = - \frac{1}{2} $$
En conclusión, reducir la función trigonométrica sen(330°) al primer cuadrante como -1 × cos(60°) simplifica notablemente el cálculo.
Y así sucesivamente.