Ángulos Asociados α y -α en Trigonometría

En trigonometría, los ángulos asociados alfa (α) y menos alfa (-α) permiten aplicar las siguientes fórmulas de transformación: $$ \sin(-\alpha) = -\sin(\alpha) $$ $$ \cos(-\alpha) = \cos(\alpha) $$ $$ \tan(-\alpha) = -\tan(\alpha) $$ $$ \cot(-\alpha) = -\cot(\alpha) $$

Esto se debe a que los ángulos asociados α y -α tienen el mismo valor absoluto en sus funciones trigonométricas - seno, coseno, tangente y cotangente - lo que permite describir sus relaciones mediante estas fórmulas.

Explicación y demostración

Consideremos un ángulo α y su opuesto, -α, situados sobre la circunferencia unitaria.

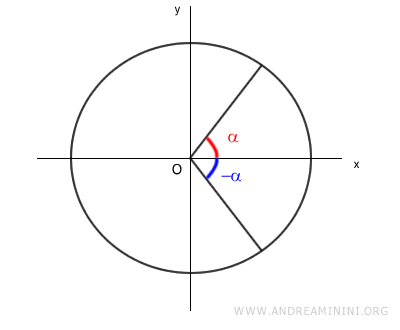
Los ángulos α y -α se denominan ángulos opuestos.

Analicemos ahora el comportamiento de las funciones trigonométricas en estos ángulos.

Seno

Los ángulos opuestos α y -α generan valores de seno iguales en magnitud pero de signo contrario sobre el eje y: sen(α) y sen(-α).

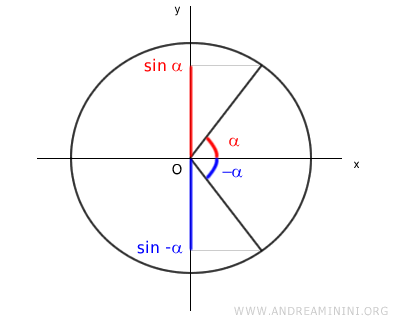
Al ser ángulos asociados, el valor absoluto del seno es idéntico para ambos:

$$ \sin \alpha = \big| \sin(-\alpha) \big| $$

Dado que el seno es una función impar, es decir, f(-x) = -f(x), se cumple que:

$$ \sin(-\alpha) = -\sin(\alpha) $$

Ambas expresiones representan exactamente la misma relación.

Coseno

En el caso de los ángulos opuestos α y -α, la función coseno produce el mismo valor sobre el eje x: cos(α) y cos(-α).

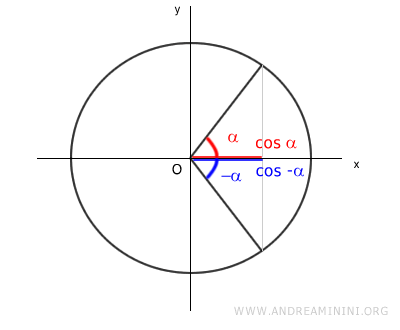
También en este caso, el valor absoluto del coseno coincide:

$$ \cos \alpha = \big| \cos(-\alpha) \big| $$

Como el coseno es una función par, es decir, f(-x) = f(x), se cumple que:

$$ \cos(-\alpha) = \cos(\alpha) $$

Ambas fórmulas expresan exactamente la misma propiedad.

Comprendidas las equivalencias en seno y coseno para α y -α, podemos deducir fácilmente las de tangente y cotangente.

Tangente

La tangente de un ángulo se define como el cociente entre el seno y el coseno:

$$ \tan \alpha = \frac{\sin \alpha}{\cos \alpha} $$

Para el ángulo -α, la tangente se expresa así:

$$ \tan(-\alpha) = \frac{\sin(-\alpha)}{\cos(-\alpha)} $$

Sustituyendo las identidades conocidas, sen(-α) = -sen(α) y cos(-α) = cos(α), obtenemos:

$$ \tan(-\alpha) = \frac{-\sin \alpha}{\cos \alpha} $$

Por lo tanto, la tangente de -α es igual a menos la tangente de α:

$$ \tan(-\alpha) = -\tan(\alpha) $$

Procedamos ahora a demostrar la relación para la cotangente, que es el recíproco de la tangente.

Cotangente

La cotangente de un ángulo es el cociente entre el coseno y el seno:

$$ \cot \alpha = \frac{\cos \alpha}{\sin \alpha} $$

Para el ángulo -α se cumple:

$$ \cot(-\alpha) = \frac{\cos(-\alpha)}{\sin(-\alpha)} $$

Usando las identidades sen(-α) = -sen(α) y cos(-α) = cos(α), se obtiene:

$$ \cot(-\alpha) = \frac{\cos \alpha}{-\sin \alpha} $$

Por tanto, la cotangente de -α es igual a menos la cotangente de α:

$$ \cot(-\alpha) = -\cot(\alpha) $$

Con esto, quedan demostradas todas las fórmulas de transformación entre α y -α.

Un ejemplo práctico

Calculemos el seno de -30°:

$$ \sin(-30°) $$

Expresado en radianes, equivale a:

$$ \sin(-30°) = \sin\left(-\frac{\pi}{6}\right) $$

Dado que los ángulos opuestos α = π/6 y -α = -π/6 son ángulos asociados, se cumple que:

$$ \sin(-\alpha) = -\sin(\alpha) $$

Por tanto, el seno de -30° es el opuesto del seno de 30°:

$$ \sin(-30°) = \sin\left(-\frac{\pi}{6}\right) = -\sin\left(\frac{\pi}{6}\right) $$

Como sabemos que el seno de 30° es 1/2, entonces el seno de -30° es -1/2:

$$ \sin(-30°) = -\frac{1}{2} $$

Y así sucesivamente.