Ángulos Asociados: α y 3π/2 - α en Trigonometría
En trigonometría, los ángulos alfa (α) y 3π/2 - α son ángulos asociados que permiten aplicar las siguientes fórmulas de transformación: $$ \sin\left( \frac{3 \pi}{2} - \alpha \right) = - \cos(\alpha) $$ $$ \cos\left( \frac{3 \pi}{2} - \alpha \right) = - \sin(\alpha) $$ $$ \tan\left( \frac{3 \pi}{2} - \alpha \right) = \cot(\alpha) $$ $$ \cot\left( \frac{3 \pi}{2} - \alpha \right) = \tan(\alpha) $$
Los ángulos α y 3π/2 - α son ángulos asociados, lo que significa que tienen el mismo valor absoluto en las funciones trigonométricas seno, coseno, tangente y cotangente, aunque sus signos pueden variar.
Demostración y explicación
Consideremos el ángulo α y el ángulo 3π/2 - α sobre la circunferencia unitaria.
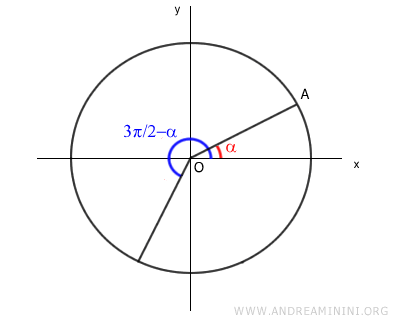
Construimos dos triángulos rectángulos, OAB y OCD, en la circunferencia unitaria.
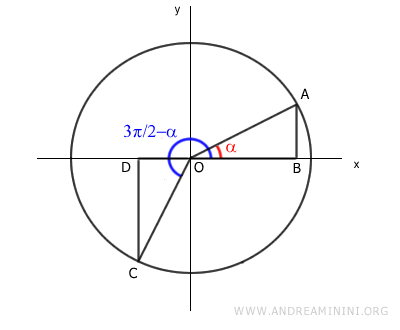
Estos triángulos, OAB y OCD, son congruentes, pues comparten el mismo ángulo agudo (α) y la misma longitud de hipotenusa.
Esto implica que sus lados correspondientes miden lo mismo.
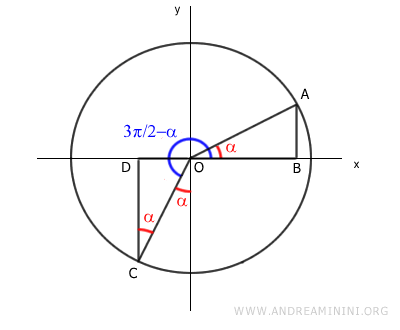
Nota: Sabemos que la suma de los ángulos de un triángulo es π (180°). En el triángulo OCD, uno de los ángulos es recto (π/2 o 90°), y otro es (π/2 - α). Por tanto, el ángulo restante es α: $$ \pi = \frac{\pi}{2} + \left(\frac{\pi}{2} - \alpha \right) + \alpha $$
El segmento CD es igual al segmento OB.
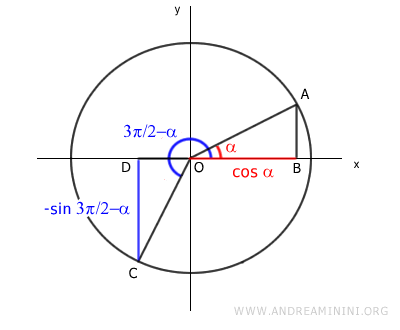
Aquí, el segmento CD representa el seno de 3π/2 - α sobre el eje y negativo, mientras que el segmento OB representa el coseno de α sobre el eje x positivo.
$$ - \sin\left( \frac{3 \pi}{2} - \alpha \right) = \cos \alpha $$
Multiplicando ambos lados por -1 se obtiene:
$$ \sin\left( \frac{3 \pi}{2} - \alpha \right) = - \cos \alpha $$
Por tanto, el seno de 3π/2 - α es igual al opuesto del coseno de α:
$$ \sin\left( \frac{3 \pi}{2} - \alpha \right) = - \cos \alpha $$
Del mismo modo, el segmento AB es igual al segmento OD.
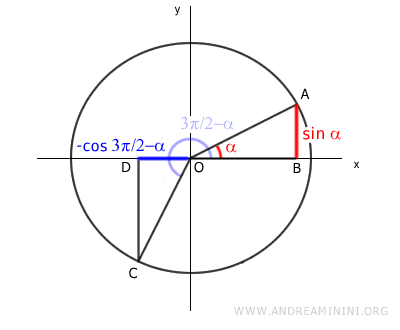
En este caso, el segmento OD mide el coseno de 3π/2 - α sobre el eje x negativo, mientras que el segmento AB mide el seno de α sobre el eje y positivo.
$$ - \cos\left( \frac{3 \pi}{2} - \alpha \right) = \sin \alpha $$
Multiplicando ambos lados por -1 se obtiene:
$$ \cos\left( \frac{3 \pi}{2} - \alpha \right) = - \sin \alpha $$
Así, el coseno de 3π/2 - α es igual al opuesto del seno de α:
$$ \cos\left( \frac{3 \pi}{2} - \alpha \right) = - \sin \alpha $$
Conociendo las fórmulas de transformación para seno y coseno, podemos deducir las de tangente y cotangente.
La tangente se define como el cociente entre seno y coseno:
$$ \tan\left( \frac{3 \pi}{2} - \alpha \right) = \frac{ \sin\left( \frac{3 \pi}{2} - \alpha \right) }{ \cos\left( \frac{3 \pi}{2} - \alpha \right) } $$
Como sen(3π/2 - α) = - cos(α) y cos(3π/2 - α) = - sen(α), resulta que:
$$ \tan\left( \frac{3 \pi}{2} - \alpha \right) = \frac{ - \cos \alpha }{ - \sin \alpha } = \cot \alpha $$
Por tanto, la tangente de 3π/2 - α es igual a la cotangente de α.
La cotangente se define como el cociente entre coseno y seno:
$$ \cot\left( \frac{3 \pi}{2} - \alpha \right) = \frac{ \cos\left( \frac{3 \pi}{2} - \alpha \right) }{ \sin\left( \frac{3 \pi}{2} - \alpha \right) } $$
Como sen(3π/2 - α) = - cos(α) y cos(3π/2 - α) = - sen(α), se obtiene:
$$ \cot\left( \frac{3 \pi}{2} - \alpha \right) = \frac{ - \sin \alpha }{ - \cos \alpha } = \tan \alpha $$
Por tanto, la cotangente de 3π/2 - α es igual a la tangente de α.
Ejemplo práctico
Calculemos el seno de 210°:
$$ \sin 210° $$
Podemos expresar este ángulo como la diferencia 270° - 60°:
$$ \sin\left( 270° - 60° \right) $$
En radianes, esto se escribe así:
$$ \sin\left( \frac{3 \pi}{2} - \frac{\pi}{3} \right) $$
Los ángulos 3π/2 - α y α son ángulos asociados, donde α = π/3 (equivalente a 60°).
$$ \sin\left( \frac{3 \pi}{2} - \alpha \right) = - \cos(\alpha) $$
$$ \sin\left( \frac{3 \pi}{2} - \frac{\pi}{3} \right) = - \cos\left( \frac{\pi}{3} \right) $$
Por tanto, el seno de 210° es igual al opuesto del coseno de 60°.
Como el coseno de 60° es 1/2, su opuesto es -1/2:
$$ \sin\left( \frac{3 \pi}{2} - \frac{\pi}{3} \right) = - \cos\left( \frac{\pi}{3} \right) = - \frac{1}{2} $$
Así que el seno de 210° es -1/2:
$$ \sin 210° = - \frac{1}{2} $$
Reducir la función trigonométrica sen(210°) al primer cuadrante, expresándola como -cos(60°), facilita notablemente el cálculo.
Y así sucesivamente.