Ángulos Asociados: α y π-α en Trigonometría
En trigonometría, los ángulos alfa (α) y π-α permiten aplicar las siguientes fórmulas de transformación: $$ \sin(\pi-\alpha) = \sin(\alpha) $$ $$ \cos(\pi-\alpha) = -\cos(\alpha) $$ $$ -\tan(\pi-\alpha) = \tan(\alpha) $$ $$ -\cot(\pi-\alpha) = \cot(\alpha) $$
Por tratarse de ángulos asociados, α y π-α presentan el mismo valor absoluto en las funciones trigonométricas seno, coseno, tangente y cotangente.
Demostración y explicación
Consideremos un ángulo α y su ángulo asociado π-α en una circunferencia unitaria.
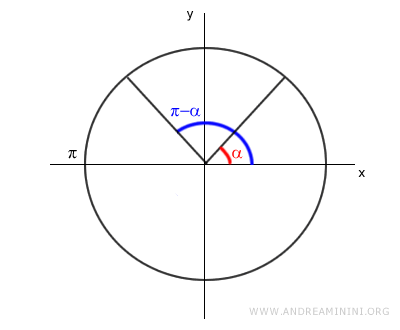
Los ángulos α y π-α son ángulos suplementarios ya que su suma equivale a 180° (π).
$$ \alpha + (\pi - \alpha) = \pi $$
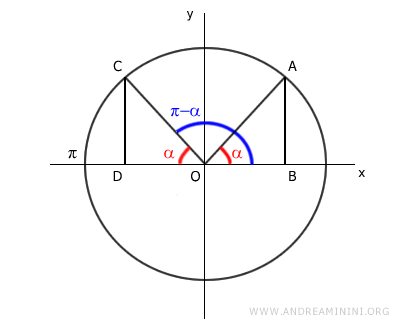
Por esta razón, los triángulos rectángulos OAB y OCD son congruentes, pues poseen la misma hipotenusa (OA = OC), el mismo ángulo agudo (α) y, naturalmente, un ángulo recto (90°).
Ambos triángulos, OAB y OCD, tienen lados y ángulos exactamente iguales.
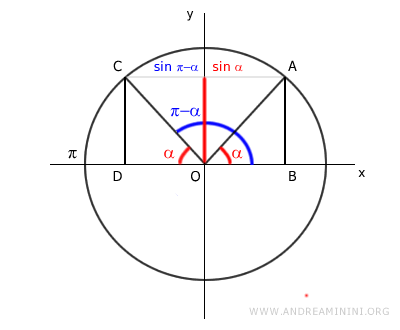
Por consiguiente, los ángulos suplementarios α y π-α presentan el mismo valor en la función seno, ya que las alturas de ambos triángulos son iguales (AB = CD).
$$ \sin \alpha = \sin (\pi - \alpha) $$
Esto se aprecia fácilmente de manera gráfica.
Asimismo, los ángulos α y π-α comparten el mismo valor absoluto en la función coseno (OB = OD).
No obstante, los valores del coseno son opuestos, ya que OD se encuentra en el semieje negativo del eje x, mientras que OB se sitúa en el semieje positivo.
$$ \cos \alpha = - \cos (\pi - \alpha) $$
Multiplicando ambos lados de la ecuación por -1, obtenemos:
$$ - (1) \cdot \cos \alpha = (-1) \cdot (- \cos (\pi - \alpha)) $$
$$ - \cos \alpha = \cos (\pi - \alpha) $$
Este hecho también se puede visualizar gráficamente.
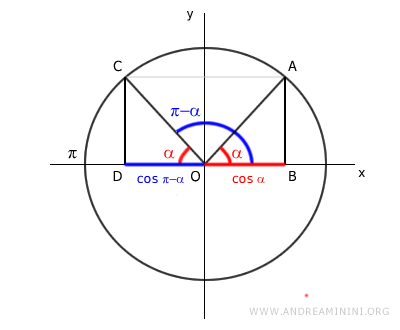
En definitiva, los cosenos de los ángulos asociados α y π-α tienen signos contrarios.
A partir de estas relaciones, podemos deducir las fórmulas de transformación para la tangente y la cotangente.
La tangente se define como el cociente entre el seno y el coseno:
$$ \tan (\pi - \alpha) = \frac{\sin (\pi - \alpha)}{\cos (\pi - \alpha)} $$
Dado que sen(π-α) = sen(α) y cos(π-α) = -cos(α), se obtiene:
$$ \tan (\pi - \alpha) = \frac{\sin \alpha}{- \cos \alpha} = - \tan \alpha $$
Por lo tanto, la tangente de π-α es el opuesto de la tangente de α.
Por su parte, la cotangente se define como el cociente entre el coseno y el seno:
$$ \cot (\pi - \alpha) = \frac{\cos (\pi - \alpha)}{\sin (\pi - \alpha)} $$
Sabiendo que sen(π-α) = sen(α) y cos(π-α) = -cos(α), se deduce:
$$ \cot (\pi - \alpha) = \frac{- \cos \alpha}{\sin \alpha} = - \cot \alpha $$
Por tanto, la cotangente de π-α es el opuesto de la cotangente de α.
En conclusión, la tangente y la cotangente de los ángulos asociados α y π-α tienen signos opuestos.
Ejemplo práctico
Calculemos el seno de 150°:
$$ \sin 150° $$
Podemos expresar este ángulo como 180° - 30°:
$$ \sin 150° = \sin (180° - 30°) $$
En radianes, se escribe así:
$$ \sin 150° = \sin \left( \pi - \frac{\pi}{6} \right) $$
Los ángulos π-α y α son ángulos asociados, donde α = π/6 (equivalente a 30°).
$$ \sin(\pi - \alpha) = \sin(\alpha) $$
Por lo tanto, el seno de 150° es igual al seno de 30°:
$$ \sin 150° = \sin \left( \pi - \frac{\pi}{6} \right) = \sin \left( \frac{\pi}{6} \right) $$
Como el seno de 30° es 1/2, el seno de 150° también es 1/2:
$$ \sin 150° = \frac{1}{2} $$
Y así sucesivamente.