Matriz triangular inferior
Una matriz cuadrada se denomina matriz triangular inferior cuando todos los elementos situados por encima de la diagonal principal son iguales a cero: $$ \forall \ i < j \ \ \ \ a_{ij} = 0 $$
Ejemplo práctico
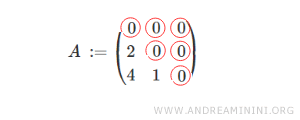
Consideremos una matriz triangular inferior de orden 3, es decir, con tres filas y tres columnas.
Como puede observarse, todos los elementos por encima de la diagonal principal son nulos.

Nota: Los elementos situados sobre la diagonal o por debajo de ella no están sujetos a ninguna restricción: pueden ser cero o no.
Si, además, todos los elementos de la diagonal principal son iguales a cero, la matriz se denomina matriz estrictamente triangular inferior.
El conjunto de matrices triangulares inferiores con coeficientes reales y de orden \( n \) se denota mediante \( T_{R} \).
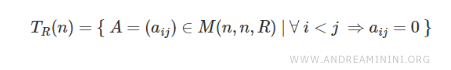
Nota: Las matrices triangulares reducen la complejidad computacional, ya que la información se concentra en una sola región de la matriz. Esto implica menos operaciones aritméticas y un uso más eficiente de la memoria.
¿Por qué utilizar matrices triangulares inferiores?
En una matriz triangular inferior, los elementos distintos de cero se agrupan exclusivamente en la parte inferior de la matriz. Esto permite representar la información con mayor eficiencia, tanto en términos de almacenamiento como de procesamiento.
Además, el determinante de una matriz triangular puede calcularse directamente como el producto de los elementos de su diagonal principal, ya que todos los demás términos no afectan al resultado.
Y así sucesivamente.