Matriz triangular superior
Una matriz cuadrada se denomina matriz triangular superior cuando todos los elementos ubicados por debajo de la diagonal principal son cero: $$ \forall \ i > j \ \ \ \ a_{ij} = 0 $$
Ejemplo práctico
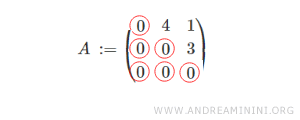
Consideremos una matriz de orden 3 (3 filas y 3 columnas) que cumple esta propiedad.
Obsérvese que todos los elementos situados por debajo de la diagonal principal son nulos.

Nota: Los elementos situados sobre la diagonal, así como la diagonal misma, pueden ser nulos o no; no existe ninguna restricción al respecto.
Si además todos los elementos de la diagonal principal son cero, se dice que la matriz es estrictamente triangular superior.
El conjunto de matrices triangulares superiores con entradas reales de orden \( n \) se denota habitualmente como \( T^R \).
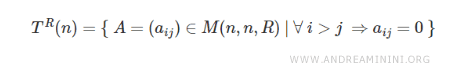
¿Por qué son importantes las matrices triangulares superiores?
Las matrices triangulares superiores resultan especialmente útiles en el álgebra lineal porque permiten simplificar de forma significativa diversos cálculos matriciales. Al concentrarse toda la información relevante en la parte superior de la matriz, se reducen tanto el número de operaciones necesarias como la complejidad computacional.
Una propiedad destacada es que el determinante de una matriz triangular superior se obtiene directamente como el producto de los elementos de su diagonal principal, ya que todos los demás términos no aportan valor al determinante.
Y así sucesivamente.