Propiedades del determinante

El determinante de una matriz presenta las siguientes propiedades fundamentales:

El determinante de la matriz traspuesta, det(A^T), coincide con el determinante de la matriz original, det(A).

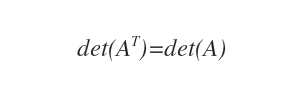
Ejemplo. En la matriz siguiente, trasponerla no modifica el valor del determinante.
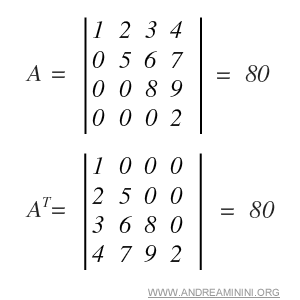
Si una matriz es triangular (superior o inferior), su determinante se obtiene simplemente multiplicando los elementos de la diagonal principal.

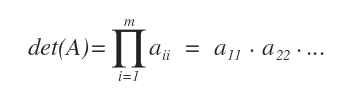
Ejemplo. En estos casos, el cálculo del determinante resulta mucho más sencillo y rápido.
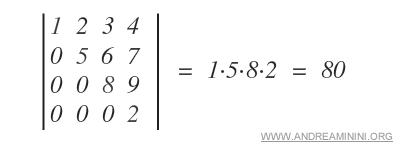
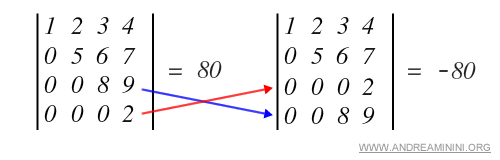
Al intercambiar dos filas o dos columnas, el determinante cambia de signo.
Ejemplo.
Multiplicar una fila o una columna por un escalar $ \alpha $ multiplica también el determinante por ese mismo factor: det($\alpha$A) = $\alpha$ det(A).

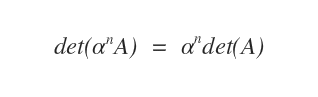
Ejemplo. En este caso, la cuarta fila R₄ se multiplica por 2, lo que provoca que el determinante también se duplique.
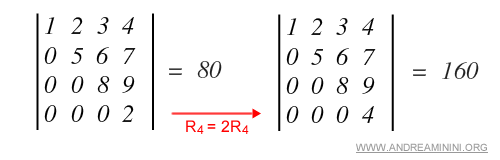
Si a una fila se le suma un múltiplo de otra (o a una columna un múltiplo de otra), el determinante permanece inalterado.
Ejemplo. Aquí, la cuarta fila R₄ se reemplaza sumándole dos veces la primera fila R₁.
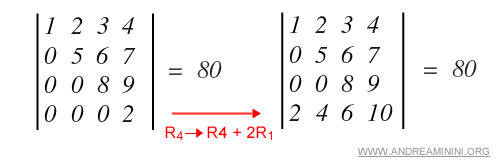
El determinante de una matriz es nulo en los siguientes casos:

a) Una fila o una columna está formada únicamente por ceros.

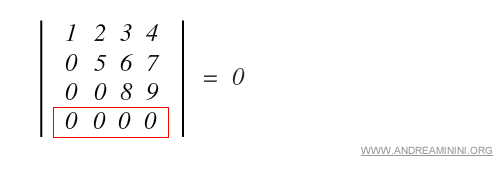
b) Dos filas o dos columnas son idénticas.

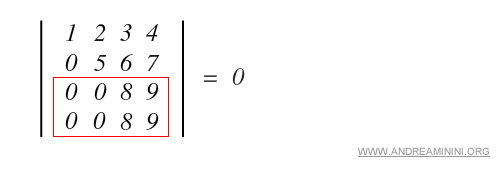
c) Dos filas o dos columnas son proporcionales.

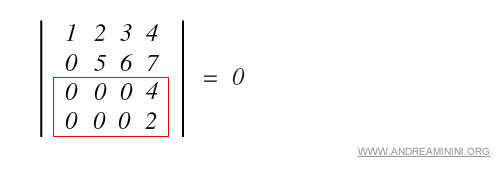
Nota. Si una fila o una columna puede expresarse como combinación lineal de las demás, la matriz es linealmente dependiente, lo que implica que su determinante es cero.
El determinante del producto de dos matrices cumple la identidad: det(AB) = det(A) det(B) ( Teorema de Binet ).
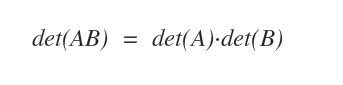
El determinante de la inversa de una matriz es el recíproco de su determinante: det(A^-1) = 1/det(A).

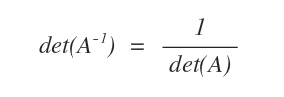
Demostración. Según el teorema de Binet, el determinante de un producto A·B es igual al producto de sus determinantes: $$ det(A \cdot B) = det(A) \cdot det(B) $$ Aplicando esto a una matriz A invertible y a su inversa A^-1: $$ det(A \cdot A^{-1}) = det(A^{-1}) \cdot det(A) $$ Como el producto de una matriz por su inversa es la matriz identidad, se cumple que: $$ det(A \cdot A^{-1}) = det(I) $$ El determinante de la matriz identidad es 1; por lo tanto: $$ det(A) \cdot det(A^{-1}) = 1 $$ En consecuencia: $$ det(A^{-1}) = \frac{1}{det(A)} $$ Con esto queda demostrada la propiedad.

Y así sucesivamente.