Équation d’un plan défini par trois points non collinéaires
Étant donnés trois points distincts et non collinéaires de l’espace R3, il existe un unique plan qui les contient : P1, P2 et P3. $$ P_1 \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} $$
Détermination des équations paramétriques d’un plan
Considérons trois points $ P_1(x_1,y_1,z_1) $, $ P_2(x_2,y_2,z_2) $ et $ P_3(x_3,y_3,z_3) $. Si le plan n’est pas parallèle à l’axe $ z $, il peut s’écrire sous forme explicite :
$$ z = mx + ny + q $$
En remplaçant les coordonnées des trois points dans cette expression, on obtient un système de trois équations linéaires :
$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$
La résolution de ce système permet de déterminer les coefficients $ m $, $ n $ et $ q $, qui définissent alors l’équation du plan.
Remarque. Cette approche n’est valable que si le plan peut effectivement être mis sous forme explicite, autrement dit s’il n’est pas vertical (parallèle à l’axe $ z $).
Comment savoir si le système est résoluble ?
Pour vérifier si le système admet une solution - c’est-à-dire si les trois points définissent bien un plan que l’on peut écrire sous la forme $ z = mx + ny + q $ - on le réécrit en notation matricielle :
$$
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
m \\
n \\
q
\end{bmatrix}
=
\begin{bmatrix}
z_1 \\
z_2 \\
z_3
\end{bmatrix}
$$
Ici, $ A $ désigne la matrice des coefficients :
$$
A =
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
$$
Le système possède une solution unique si, et seulement si, le déterminant de $ A $ est non nul :
$\det(A) \ne 0$
Dans ce cas, le plan n’est pas parallèle à l’axe $ z $ et peut être écrit sous forme explicite.
En revanche, si $ \det(A) = 0 $, le plan est vertical et ne peut pas s’exprimer de cette manière. Il reste néanmoins possible d’en obtenir l’équation implicite sous la forme $ ax + by + cz + d = 0 $ par une autre méthode.
Interprétation géométrique de $ \det(A) = 0 $. Un déterminant nul signifie que les projections des trois points sur le plan $ xy $ sont alignées, autrement dit que les points projetés $ (x_i, y_i) $ appartiennent à une même droite. Dans ce cas, le plan est dit « vertical » et ne peut se représenter sous la forme $ z = mx + ny + q $.
Exemple
Considérons les trois points suivants, non collinéaires :
$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$
Le système associé s’écrit :
$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$
$$ \begin{cases} m(1) + n(3) + q = 5 \\ m(2) + n(0) + q = 3 \\ m(4) + n(1) + q =2 \end{cases} $$
$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$
La matrice des coefficients $ A $ est :
$$
A =
\begin{bmatrix}
1 & 3 & 1 \\
2 & 0 & 1 \\
4 & 1 & 1
\end{bmatrix}
$$
Son déterminant vaut :
$$ \Delta = (1 \cdot 0 \cdot 1) + (3 \cdot 1 \cdot 4) + (1 \cdot 2 \cdot 1) - (1 \cdot 0 \cdot 4) - (3 \cdot 2 \cdot 1) - (1 \cdot 1 \cdot 1) $$
$$ \Delta = 0 + 12 + 2 - 0 - 6 - 1 = 7 $$
Comme $ \Delta = 7 \ne 0 $, le système admet bien une solution unique.
$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q = 2 \end{cases} $$
Résolvons-le à l’aide de la règle de Cramer.
On commence par remplacer la première colonne par les termes constants $ (5,3,2) $ :
$$ \Delta_m = \begin{vmatrix} 5 & 3 & 1 \\ 3 & 0 & 1 \\ 2 & 1 & 1 \end{vmatrix} $$
$$ \Delta_m = 5 \cdot \begin{vmatrix} 0 & 1 \\ 1 & 1 \end{vmatrix} - 3 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 3 & 0 \\ 2 & 1 \end{vmatrix} $$
$$ \Delta_m = 5(-1) - 3(1) + 1(3) = -5 - 3 + 3 $$
$$ \Delta_m = -5 $$
Puis, on remplace la deuxième colonne :
$$ \Delta_n = \begin{vmatrix} 1 & 5 & 1 \\ 2 & 3 & 1 \\ 4 & 2 & 1 \end{vmatrix} $$
$$ \Delta_n = 1 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} - 5 \cdot \begin{vmatrix} 2 & 1 \\ 4 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} $$
$$ \Delta_n = 1(1) - 5(-2) + 1(-8) = 1 + 10 - 8 $$
$$ \Delta_n = 3 $$
Enfin, on remplace la troisième colonne :
$$ \Delta_q = \begin{vmatrix} 1 & 3 & 5 \\ 2 & 0 & 3 \\ 4 & 1 & 2 \end{vmatrix} $$
$$ \Delta_q = 1 \cdot \begin{vmatrix} 0 & 3 \\ 1 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 2 & 0 \\ 4 & 1 \end{vmatrix} $$
$$ \Delta_q = 1(-3) - 3(-8) + 5(2) = -3 + 24 + 10 $$
$$ \Delta_q = 31 $$
On applique alors la règle de Cramer :
$$ m = \frac{\Delta_m}{\Delta} = \frac{-5}{7} $$
$$ n = \frac{\Delta_n}{\Delta} = \frac{3}{7} $$
$$ q = \frac{\Delta_q}{\Delta} = \frac{31}{7} $$
On obtient ainsi :
$$ \begin{cases} m = -\frac{5}{7} \\ n = \frac{3}{7} \\ q = \frac{31}{7} \end{cases} $$
En substituant $ m $, $ n $ et $ q $ dans l’équation explicite du plan $ z = mx + ny + q $, il vient :
$$ -\frac{5}{7} x + \frac{3}{7}y + \frac{31}{7} = z $$
Voici donc l’équation du plan passant par les points $ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $
Une méthode alternative, plus générale
Cette approche permet de déterminer l’équation générale (ou implicite) d’un plan à partir de trois points donnés :
$a x + b y + c z + d = 0$
Son principal atout est son universalité : elle s’applique que le plan soit vertical, horizontal ou oblique, et elle évite la résolution d’un système d’équations.
En revanche, elle suppose une connaissance minimale de l’algèbre et du calcul vectoriel.
Procédure
On considère les coordonnées de trois points de l’espace :
$$
P_1(x_1,y_1,z_1), \quad
P_2(x_2,y_2,z_2), \quad
P_3(x_3,y_3,z_3)
$$
À partir de ces points, on forme deux vecteurs directeurs appartenant au plan :
$$ \vec{v_1} = P_2 - P_1 = (x_2 - x_1, \ y_2 - y_1, \ z_2 - z_1) $$
$$ \vec{v_2} = P_3 - P_1 = (x_3 - x_1, \ y_3 - y_1, \ z_3 - z_1) $$
Le produit vectoriel $ \vec{n} = \vec{v_1} \times \vec{v_2} $ fournit alors un vecteur normal au plan :
$$
\vec{n} = (a, b, c) =
\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\
x_3 - x_1 & y_3 - y_1 & z_3 - z_1
\end{matrix}
\right|
$$
Les composantes de ce vecteur normal correspondent directement aux coefficients $ a $, $ b $ et $ c $ de l’équation générale du plan.
On peut aussi obtenir ces coefficients par les formules suivantes :
$$ a = (y_2 - y_1)(z_3 - z_1) - (y_3 - y_1)(z_2 - z_1) $$
$$ b = (z_2 - z_1)(x_3 - x_1) - (z_3 - z_1)(x_2 - x_1) $$
$$ c = (x_2 - x_1)(y_3 - y_1) - (x_3 - x_1)(y_2 - y_1) $$
Une fois $ a $, $ b $ et $ c $ connus, on peut écrire l’équation générale du plan en utilisant l’un des trois points :
$$ a (x - x_1) + b (y - y_1) + c (z - z_1) = 0 $$
En développant, on retrouve la forme implicite :
$$ a x + b y + c z + d = 0 $$
où la constante $ d $ est donnée par :
$$ d = - (a x_1 + b y_1 + c z_1) $$
Ces deux écritures sont équivalentes.
Si de plus $ c \ne 0 $, on peut isoler $ z $ et obtenir la forme explicite du plan :
$$ z = - \frac{a}{c} x - \frac{b}{c} y - \frac{d}{c} $$
Bien entendu, si $ c = 0 $, le plan est vertical par rapport à l’axe $ z $ et ne peut pas s’exprimer de cette manière.
Exemple
Reprenons les trois points de l’exemple précédent :
$$
P_1 = (1, 3, 5), \quad
P_2 = (2, 0, 3), \quad
P_3 = (4, 1, 2)
$$
Les vecteurs directeurs du plan sont :
$$ \vec{v_1} = P_2 - P_1 = (1, \ -3, \ -2) $$
$$ \vec{v_2} = P_3 - P_1 = (3, \ -2, \ -3) $$
Leur produit vectoriel vaut :
$$ \vec{n} = \vec{v_1} \times \vec{v_2} = (a, b, c) $$
En développant le déterminant :
$$ \vec{n} = \left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -3 & -2 \\ 3 & -2 & -3 \end{matrix} \right| $$
$$ \vec{n} = \mathbf{i}(9 - 4) - \mathbf{j}(-3 + 6) + \mathbf{k}(-2 - (-9)) $$
$$ \vec{n} = 5 \mathbf{i} + 3 \mathbf{j} + 7 \mathbf{k} $$
Le vecteur normal au plan est donc $ \vec{n} = (5, 3, 7) $.
On en déduit les coefficients :
$$ a = 5, \quad b = 3, \quad c = 7 $$
L’équation du plan s’écrit :
$$ 5(x - 1) + 3(y - 3) + 7(z - 5) = 0 $$
En développant :
$$ 5x - 5 + 3y - 9 + 7z - 35 = 0 $$
$$ 5x + 3y + 7z - 49 = 0 $$
L’équation générale du plan est donc :
$$ 5x + 3y + 7z = 49 $$
Comme le coefficient de $ z $ est non nul, on peut également donner la forme explicite :
$$ z = -\frac{5}{7} x - \frac{3}{7} y + \frac{49}{7} $$
On obtient ainsi l’équation explicite du plan passant par les trois points considérés, ce qui concorde exactement avec le résultat du premier procédé.
Méthode vectorielle
À partir de trois points de l’espace, on peut construire deux vecteurs directeurs :
$$ v_1 = P_1P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} $$
$$ v_2 = P_1P_3 = \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
Il convient d’abord de vérifier que ces vecteurs sont linéairement indépendants.
En effet, ils engendrent le plan et constituent une base du sous-espace vectoriel associé uniquement s’ils ne sont pas colinéaires.
Deux vecteurs sont indépendants lorsque le rang de la matrice obtenue en les plaçant en colonnes est égal à deux :
$$ r_k \begin{pmatrix} x_2 - x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 2 $$
Une fois l’indépendance vérifiée, on choisit un des trois points comme point de référence $P_0$ appartenant au plan.
Par exemple, on peut prendre $P_1$ :
$$ P_0 = P_1 $$
$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$
On peut alors écrire l’équation vectorielle du plan :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \, v_1 + t_2 \, v_2 $$
où $ t_1 $ et $ t_2 $ sont des paramètres réels décrivant l’ensemble des points du plan.
En remplaçant les vecteurs directeurs :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
et en précisant $P_0$ :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$
On obtient ainsi la forme paramétrique du plan, traduite en un système de trois équations :
$$ \begin{cases} x = x_0 + t_1 ( x_2 - x_1 ) + t_2 ( x_3 - x_1 ) \\ y = y_0 + t_1 ( y_2 - y_1 ) + t_2 ( y_3 - y_1 ) \\ z = z_0 + t_1 ( z_2 - z_1 ) + t_2 ( z_3 - z_1 ) \end{cases} $$
Pour dériver l’équation cartésienne, on ramène les coordonnées de $P_0$ au premier membre :
$$ \begin{cases} x - x_0 = t_1 ( x_2 - x_1 ) + t_2 ( x_3 - x_1 ) \\ y - y_0 = t_1 ( y_2 - y_1 ) + t_2 ( y_3 - y_1 ) \\ z - z_0 = t_1 ( z_2 - z_1 ) + t_2 ( z_3 - z_1 ) \end{cases} $$
On forme alors une matrice avec, en colonnes, le vecteur $ (x-x_0, y-y_0, z-z_0) $ et les deux vecteurs directeurs :
$$ \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} $$
En annulant le déterminant de cette matrice, on obtient l’équation cartésienne du plan :
$$ det \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 0 $$
$$ ( x-x_0 ) \begin{vmatrix} y_2-y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} - (y-y_0) \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} +(z-z_0) \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ y_2-y_1 & y_3 - y_1 \end{vmatrix} = 0$$
Ce qui donne finalement :
$$ ( x-x_0 ) \, a - (y-y_0) \, b + (z-z_0) \, c = 0$$
Exemple
Considérons trois points non collinéaires :
$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$
On en déduit les vecteurs directeurs :
$$ v_1 = P_1P_2 = \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} $$
$$ v_2 = P_1P_3 = \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$
On vérifie leur indépendance linéaire :
$$ r_k \begin{pmatrix} 1 & 3 \\ -3 & -2 \\ -2 & -3 \end{pmatrix} = 2 $$
Le rang ($r_k = 2$) correspond au nombre de vecteurs, ils sont donc indépendants et peuvent servir de base.
On choisit $P_1$ comme point de référence $P_0$ :
$$ P_0 = P_1 $$
$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} $$
On écrit alors l’équation vectorielle du plan :
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} + t_1 \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} + t_2 \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$
D’où les équations paramétriques :
$$ \begin{cases} x = 1 + t_1 + 3 t_2 \\ y = 3 - 3 t_1 - 2 t_2 \\ z = 5 - 2 t_1 - 3 t_2 \end{cases} $$
On obtient enfin l’équation cartésienne du plan en calculant le déterminant :
$$ det \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$
$$ ( x-1 ) \cdot 5 - (y-3) \cdot 3 +(z-5) \cdot 7 $$
$$ 5x - 3y + 7z - 31 $$
En posant l’équation égale à zéro, on obtient l’équation cartésienne du plan :
$$ 5x - 3y + 7z - 31 = 0 $$
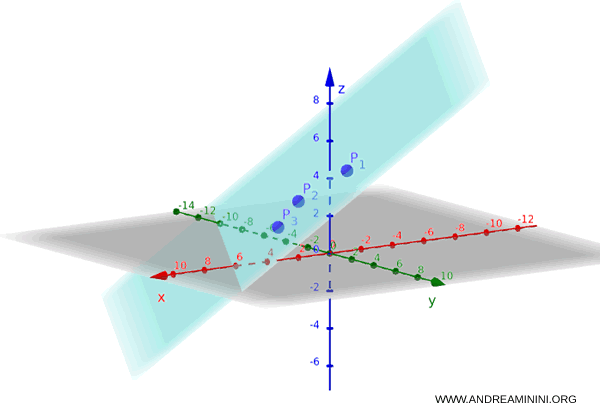
La représentation graphique du plan dans l’espace tridimensionnel est illustrée ci-dessous :

Et ainsi de suite.