Rang d’une matrice

Le rang d’une matrice A est défini comme l’ordre le plus élevé d’un mineur non nul. On parle également de la caractéristique de la matrice.

Soit une matrice A de dimensions m×n. On dit que son rang est p s’il existe au moins un mineur d’ordre p dont le déterminant est non nul, et si tous les mineurs d’ordre p+1, lorsqu’ils existent, sont nuls.

Le rang d’une matrice A est un entier réel que l’on note couramment rk(A), rg(A), r(A) ou encore p(A).

Remarque. En résumé, le rang d’une matrice correspond au plus grand ordre d’un mineur dont le déterminant n’est pas nul.

À quoi sert le rang ?

Le rang mesure combien de lignes ou de colonnes d’une matrice sont linéairement indépendantes.

Comment déterminer le rang d’une matrice

Si la matrice A appartient à M_m×n, alors son rang, noté r(A), est compris entre zéro et le minimum de m et n.

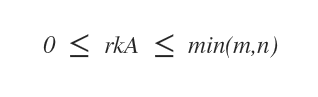
Le rang représente le nombre maximal de lignes ou de colonnes linéairement indépendantes à l’intérieur de la matrice.

Il ne peut donc pas dépasser ni le nombre total de lignes, ni celui de colonnes.

Remarque. Par convention, seule la matrice nulle a un rang nul. Toute autre matrice a un rang supérieur ou égal à un.

Un exemple concret

Examinons à présent le calcul du rang d’une matrice 3×4.

Dans cet exemple, le rang de la matrice est égal à 3.

Remarque. Pour déterminer le rang, il n’est pas nécessaire de vérifier tous les mineurs de tous les ordres. Il suffit de trouver un mineur non nul d’ordre N, puis d’examiner ceux d’ordre N+1.

Rang complet ou maximal

Une matrice est dite de rang complet ou de rang maximal lorsque son rang est égal à min(m,n).

Exemple

Voici un exemple de matrice de rang complet.

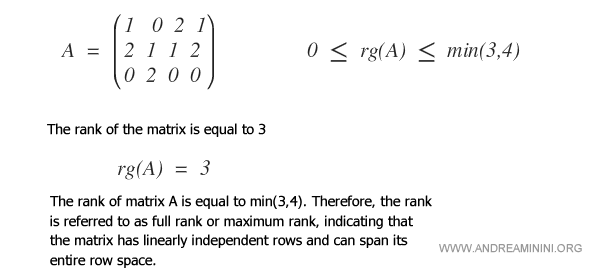
Remarque. Pour une matrice carrée d’ordre n, le rang ne peut être égal à n - autrement dit rg(A)=n - que si le déterminant de la matrice est non nul.

Propriétés du rang

Le rang d’une matrice vérifie un certain nombre de propriétés fondamentales :

1. Le rang d’une matrice A est égal à celui de sa transposée A^T.
   
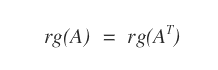
2. Le rang est nul uniquement si la matrice est entièrement nulle.
3. Si tous les mineurs d’ordre N sont nuls, alors tous les mineurs d’ordre supérieur le sont également.

   Démonstration. Supposons que tous les mineurs d’ordre k d’une matrice soient nuls, avec k inférieur au minimum de m et n (k<min{m,n}). Considérons un mineur d’ordre j, avec k<j≤min{m,n}. Par développement de Laplace, le déterminant d’ordre j se réécrit en fonction de déterminants de sous-matrices carrées d’ordre j−1. Le raisonnement se poursuit ainsi jusqu’aux déterminants d’ordre k. Comme ces derniers sont nuls, il en découle que tous les mineurs d’ordre supérieur le sont aussi.

Autres méthodes de calcul du rang

Il existe plusieurs procédés pour déterminer le rang d’une matrice.

La méthode directe consiste à calculer tous les mineurs, mais elle est souvent lourde et inefficace.

Pour simplifier, on utilise en pratique des méthodes comme le théorème de Kronecker ou l’élimination de Gauss.

Rang et interprétation vectorielle en algèbre linéaire

Le rang d’une matrice - considérée comme un ensemble de vecteurs lignes ou colonnes - indique la quantité d’information indépendante qu’elle contient dans l’espace vectoriel.

Par exemple, considérons la matrice 2×3 :

$$ M_1 = \begin{pmatrix} 1 & 0 & 3 \\ 0 & 2 & 1 \end{pmatrix} $$

Cette matrice a pour rang 2.

$$ rk(M_1)= 2 $$

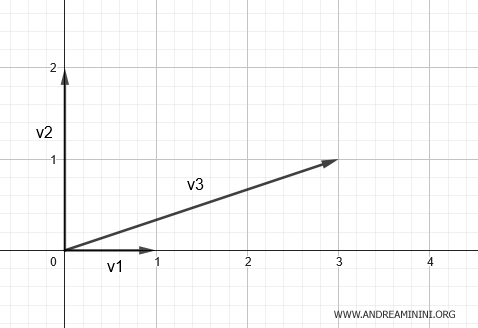
Cela signifie que les vecteurs colonnes v1=(1;0), v2=(0;2) et v3=(3;1) peuvent être représentés selon deux directions indépendantes, autrement dit, ils engendrent un plan.

Voyons un second exemple pour clarifier :

$$ M_2 = \begin{pmatrix} 2 & 4 & 6 \\ 1 & 2 & 3 \end{pmatrix} $$

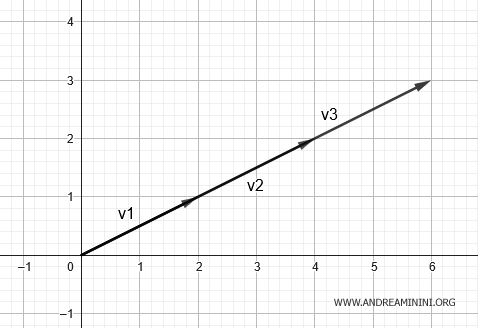
Cette matrice est de rang 1, car une ligne est un multiple de l’autre ; il existe donc une redondance.

$$ rk(M_2)= 1 $$

Autrement dit, les vecteurs v1=(2;1), v2=(4;2) et v3=(6;3) appartiennent tous à un même sous-espace unidimensionnel, c’est-à-dire à une droite.

Dans ce cas, il manque une dimension dans la représentation vectorielle.

Remarque sur les dimensions supérieures. Dans les matrices de dimension supérieure à 3, même si la représentation graphique est impossible, le rang demeure une notion essentielle pour mesurer l’indépendance entre vecteurs.

Observations

Voici quelques observations utiles concernant le rang d’une matrice :

• Deux matrices A et B sont équivalentes par lignes si et seulement si elles ont le même rang : $$ rk(A) = rk(B) $$. Cela vaut aussi bien pour les matrices carrées que rectangulaires.
• Le rang est invariant par transposition : le rang d’une matrice M est identique à celui de sa transposée M^T, autrement dit : $$ rk(M) = rk(M^T) $$