Déterminant d’une matrice

En algèbre linéaire, le déterminant d’une matrice carrée est une valeur scalaire qui renseigne sur des propriétés fondamentales de la matrice. On le note det(A) ou |A|, et il condense à la fois des aspects algébriques et géométriques.

Exemple

Considérons la matrice carrée suivante :

$$ A= \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $$

Son déterminant s’écrit :

$$ det(A) = -2 $$

Ou, en utilisant la notation avec des barres verticales :

$$ | A | = \begin{vmatrix} 1 & 2 \\ 3 & 4 \end{vmatrix} = -2 $$

Remarque. Le déterminant n’est défini que pour les matrices carrées, c’est-à-dire celles dont le nombre de lignes est égal au nombre de colonnes (m = n).

Calcul du déterminant d’une matrice

Matrices carrées d’ordre 1

Pour une matrice 1x1, qui ne comporte qu’un seul élément, le déterminant est tout simplement la valeur de cet élément, a₁₁.

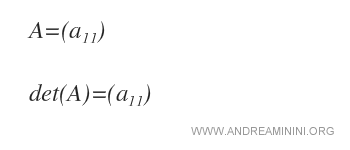
Exemple. La matrice A est d’ordre 1 et contient un seul élément : a₁₁ = 5. Ainsi, det(A) = 5.

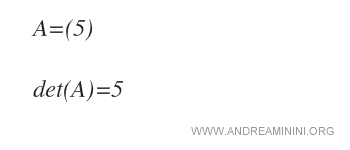
Matrices carrées d’ordre 2

Pour une matrice 2x2, on calcule le déterminant en multipliant les éléments de la diagonale principale (a₁₁·a₂₂) puis en retranchant le produit des éléments de la diagonale secondaire (a₂₁·a₁₂).

Exemple. Pour la matrice A ci-dessous, d’ordre 2, formée de deux lignes et deux colonnes, on obtient det(A) = -2.

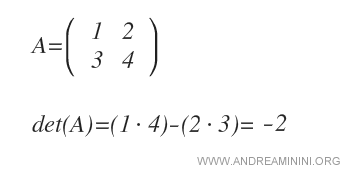
Règle de Sarrus

La règle de Sarrus est une méthode pratique pour calculer le déterminant d’une matrice carrée d’ordre 3 (3x3).

Considérons une matrice 3x3 :

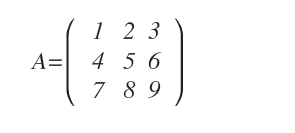
On recopie ensuite les deux premières colonnes à droite :

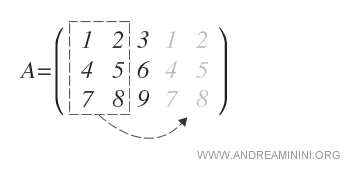
On additionne ensuite les produits des diagonales allant du coin supérieur gauche vers le coin inférieur droit :

Puis on retranche les produits des diagonales allant du coin inférieur gauche vers le coin supérieur droit :

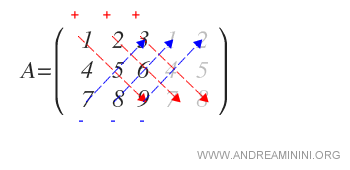
La différence de ces deux sommes donne la valeur du déterminant.

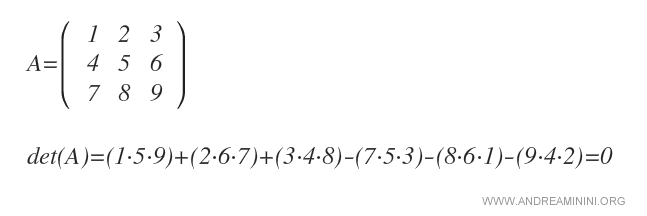
Résumé de la règle de Sarrus

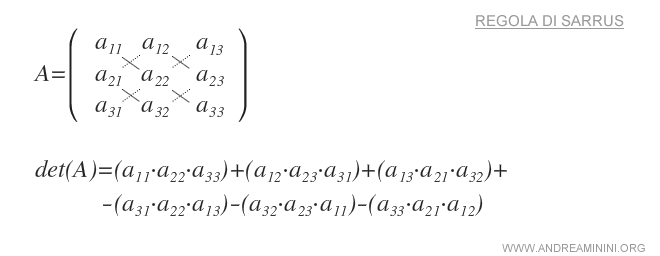
Méthode de Laplace

La méthode de Laplace est l’une des plus couramment utilisées pour le calcul des déterminants, car elle permet de ramener un déterminant d’ordre n à une combinaison de déterminants mineurs d’ordre n−1.

Elle porte le nom du mathématicien Pierre-Simon Laplace et repose sur le développement par cofacteurs.

Principe de la méthode

On exprime le déterminant comme une somme alternée de produits entre des éléments d’une ligne ou d’une colonne et les déterminants de leurs mineurs complémentaires.

1. Choisir une colonne j de la matrice.

   Quel choix privilégier ? Toutes les colonnes sont valables, mais il est conseillé de sélectionner celle qui contient le plus de zéros, ce qui simplifie considérablement les calculs.

2. Une fois la colonne j choisie, on supprime la ligne i et la colonne j associées à chaque élément, puis on calcule les déterminants des sous-matrices obtenues à l’aide de la formule de Laplace.
   

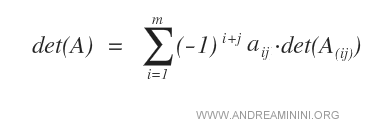
Exemple. Pour déterminer le déterminant d’une matrice A d’ordre 3, développons par cofacteurs selon la colonne j = 1. En additionnant les déterminants des mineurs correspondants, on obtient : det(A) = 0.

Développement par lignes

Le développement de Laplace peut également s’effectuer en choisissant une ligne plutôt qu’une colonne.

Dans ce cas, la formule s’applique en parcourant toutes les colonnes j de la ligne choisie.

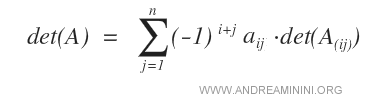
On parvient ainsi au même résultat final.

Exemple. Développons ici selon la première ligne : $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 0 & 2 & 3 \\ 0 & 5 & 1 \\ 0 & 0 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 0 & 1 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 2 \end{vmatrix} - 1 \cdot \begin{vmatrix} 0 & 1 & 2 \\ 0 & 0 & 5 \\ 0 & 0 & 0 \end{vmatrix} $$ En évaluant les mineurs : $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = 2 \cdot 10 - 3 \cdot 0 + 5 \cdot 0 - 1 \cdot 0 = 20 $$

Astuce pour gagner du temps. Pour accélérer le calcul, il est judicieux de choisir la ligne ou la colonne contenant le plus grand nombre de zéros. Dans cet exemple, on choisit la quatrième ligne : $$ \begin{vmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{vmatrix} = -0 \cdot A_{(4,1)} + 0 \cdot A_{(4,2)} - 0 \cdot A_{(4,3)} + 2 \cdot \begin{vmatrix} 2 & 3 & 5 \\ 0 & 1 & 2 \\ 0 & 0 & 5 \end{vmatrix} $$ Grâce à ces zéros, trois mineurs n’ont pas à être calculés. On répète ensuite le processus sur la troisième ligne de la sous-matrice : $$ = 2 \cdot 5 \cdot \begin{vmatrix} 2 & 3 \\ 0 & 1 \end{vmatrix} = 2 \cdot 5 \cdot (2 \cdot 1) = 20 $$ Dans ce cas précis, comme la matrice est triangulaire, on aurait aussi pu obtenir le déterminant en multipliant directement les éléments de sa diagonale principale : $$ 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Limites de la méthode de Laplace. Bien qu’efficace pour les petites matrices, cette méthode devient vite lourde pour des ordres plus élevés. Dans ce cas, il est préférable de recourir à des techniques comme l’élimination de Gauss.

Méthode d’élimination de Gauss

L’élimination de Gauss est une technique particulièrement efficace qui permet également de calculer le déterminant d’une matrice carrée.

Elle consiste à appliquer des opérations élémentaires sur les lignes afin de transformer la matrice en une forme triangulaire supérieure.

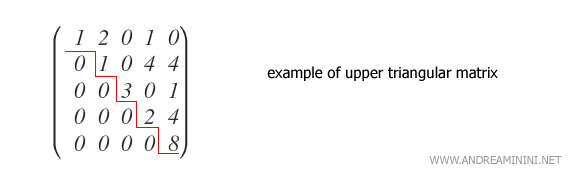
Dans une matrice triangulaire, le déterminant se calcule simplement comme le produit des éléments de la diagonale principale, ce qui rend le procédé très rapide.

Il faut néanmoins garder à l’esprit l’incidence des opérations élémentaires sur le signe et la valeur du déterminant :

• L’échange de deux lignes (Rx ⇔ Ry) inverse le signe du déterminant (multiplication par −1).
• La multiplication d’une ligne par un scalaire k multiplie le déterminant par k.
• L’ajout à une ligne d’un multiple d’une autre (Rx + k·Ry) laisse le déterminant inchangé.

Exemple. Dans l’exercice suivant, nous appliquons l’élimination de Gauss pour déterminer le déterminant de la matrice A :

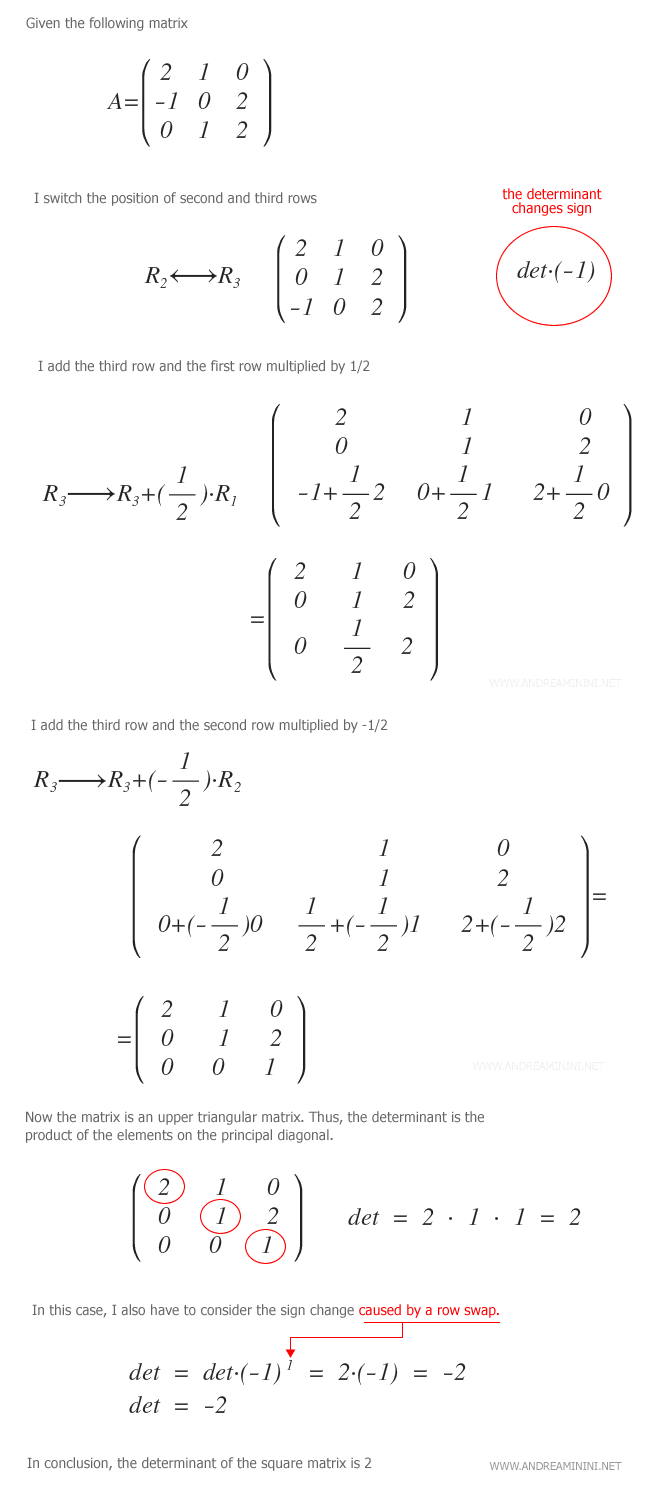
Atouts de la méthode de Gauss

Pour les matrices de grande taille, l’élimination de Gauss s’avère bien plus performante que le développement par cofacteurs de Laplace.

Propriétés du déterminant

On peut énoncer plusieurs propriétés fondamentales du déterminant des matrices carrées :

• Si une ligne ou une colonne est constituée uniquement de zéros, le déterminant est nul.

  Exemple :
  $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 7 & 8 & 9 \end{vmatrix} = 0 \quad \begin{vmatrix} 1 & 2 & 0 \\ 4 & 5 & 0 \\ 7 & 8 & 0 \end{vmatrix} = 0 $$

• Si la matrice est diagonale, triangulaire supérieure ou triangulaire inférieure, son déterminant est égal au produit des éléments de la diagonale principale.

  Exemple :
  $$ \begin{vmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{vmatrix} = 1 \cdot 5 \cdot 9 = 45 $$

• Le déterminant d’une matrice est identique à celui de sa transposée : $$ \det(A) = \det(A^T) $$

  Exemple :
  $$ \det\left(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\right) = -2 \quad \det\left(\begin{pmatrix} 1 & 3 \\ 2 & 4 \end{pmatrix}\right) = -2 $$

• Si une matrice possède deux lignes ou deux colonnes identiques, son déterminant est nul.

  Exemple :
  $$ \det\left(\begin{pmatrix} a & b \\ a & b \end{pmatrix}\right) = ab - ba = 0 $$
  $$ \det\left(\begin{pmatrix} a & b & c \\ a & b & c \\ d & e & f \end{pmatrix}\right) = 0 $$
  Le même raisonnement s’applique si deux colonnes sont identiques, puisque la transposée présente alors deux lignes identiques.

• L’échange de deux lignes (ou colonnes) change le signe du déterminant.

  Exemple :
  $$ \det\left(\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\right) = -2 $$
  $$ \det\left(\begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix}\right) = 2 $$

• Théorème de Binet : si \( A \) et \( B \) sont deux matrices carrées de même ordre, alors : $$ \det(A \cdot B) = \det(A) \cdot \det(B) $$

  Exemple :
  $$ A = \begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix},\quad B = \begin{pmatrix} 2 & 1 \\ 5 & 3 \end{pmatrix} $$
  $$ \det(A) = -10,\quad \det(B) = 1 $$
  $$ A \cdot B = \begin{pmatrix} 22 & 13 \\ 16 & 9 \end{pmatrix},\quad \det(A \cdot B) = -10 $$
  $$ \det(A) \cdot \det(B) = -10 $$

• Pour toute matrice carrée \( M \) d’ordre \( n \) et tout scalaire \( k \), on a : $$ \det(k \cdot M) = k^n \cdot \det(M) $$

  Démonstration :
  $$ k \cdot M = \begin{pmatrix} ka & kb \\ kc & kd \end{pmatrix},\quad \det(k \cdot M) = k^2 \cdot \det(M) $$
  Exemple : $$ M = \begin{pmatrix} 6 & 8 \\ 4 & 2 \end{pmatrix} = 2^2 \cdot \begin{pmatrix} 3 & 4 \\ 2 & 1 \end{pmatrix} $$
  $$ \det(M) = 4 \cdot (3 \cdot 1 - 4 \cdot 2) = -20 $$

• Si une ligne ou une colonne est un multiple exact d’une autre, le déterminant est nul.

  Exemple :
  $$ \det\left(\begin{pmatrix} 2 & 4 \\ 4 & 8 \end{pmatrix}\right) = 0 $$

Déterminant des matrices triangulaires

Le déterminant d’une matrice triangulaire se calcule comme le produit des éléments de sa diagonale principale.

En effet, tous les autres termes du développement du déterminant s’annulent.

Le calcul du déterminant d’une matrice triangulaire est donc immédiat et ne requiert aucune opération supplémentaire.

Exemple

Considérons la matrice suivante :

$$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$

Puisque \( A \) est triangulaire, son déterminant s’obtient en multipliant les éléments de la diagonale principale :

$$ \det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Observations essentielles

On peut enfin rappeler une propriété clé du déterminant :

• Le déterminant est un invariant fondamental vis-à-vis de la transposition. En d’autres termes, une matrice carrée \( M \) et sa transposée \( M^T \) ont toujours le même déterminant : $$ \det(M) = \det(M^T) $$

Calculateur de déterminants en ligne

Utilisez cet outil pour calculer le déterminant de n’importe quelle matrice carrée, de façon simple et rapide.

Et ainsi de suite