Matrice triangulaire

Une matrice carrée est dite triangulaire lorsque tous ses éléments non nuls se trouvent exclusivement au-dessus ou au-dessous de la diagonale principale.

Types de matrices triangulaires

On distingue deux types fondamentaux de matrices triangulaires : les supérieures et les inférieures.

• Triangulaire supérieure. Tous les éléments non nuls se situent au-dessus de la diagonale principale, laquelle peut contenir ou non des valeurs différentes de zéro.
  
  

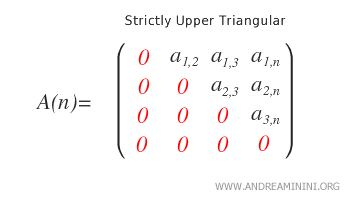
  Triangulaire supérieure stricte. Une matrice est strictement triangulaire supérieure lorsque tous ses éléments non nuls se trouvent strictement au-dessus de la diagonale principale, tandis que cette dernière et l’ensemble des éléments situés en dessous valent zéro. Formellement, pour chaque coefficient \( a_{ij} \), on a \( i < j \).
  

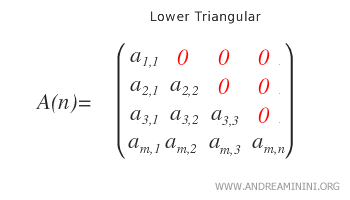
• Triangulaire inférieure. Une matrice est triangulaire inférieure si tous ses éléments non nuls apparaissent en dessous de la diagonale principale, qui peut elle-même contenir des valeurs non nulles.
  
  

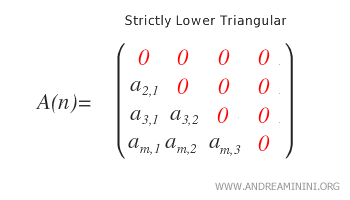
  Triangulaire inférieure stricte. Une matrice est strictement triangulaire inférieure lorsque tous ses éléments non nuls se trouvent uniquement en dessous de la diagonale principale, laquelle est composée exclusivement de zéros. Autrement dit, pour chaque coefficient non nul, on a \( i > j \).
  

Propriétés des matrices triangulaires

Parmi les propriétés essentielles de ce type de matrices, on peut retenir notamment :

• Déterminant
  Le déterminant d’une matrice triangulaire, qu’elle soit supérieure ou inférieure, est donné par le produit des éléments de sa diagonale principale.

  Exemple : Considérons la matrice triangulaire suivante : $$ A = \begin{pmatrix} 2 & 3 & 5 & 1 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 5 & 1 \\ 0 & 0 & 0 & 2 \end{pmatrix} $$ Comme les coefficients hors diagonale n’interviennent pas dans le calcul, le déterminant s’obtient en multipliant les éléments diagonaux : $$ \det(A) = 2 \cdot 1 \cdot 5 \cdot 2 = 20 $$

Et ainsi de suite...