Opération de pivot dans une matrice

L’opération de pivot est une transformation matricielle qui consiste à remplacer la colonne k d’une matrice de dimensions m × n par la colonne h de la matrice identité d’ordre m.

Pour réaliser cette opération, on commence par choisir un élément non nul de la matrice, appelé pivot. Si cet élément est nul, il ne peut pas être utilisé comme pivot.

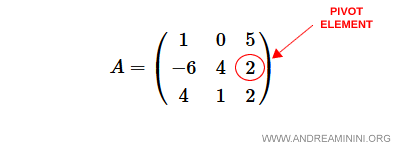
L’opération de pivot s’effectue en deux étapes principales :

1. On divise chaque entrée de la ligne h par l’élément pivot $a_{hk}$, de façon à obtenir $1$ en position de pivot : $$ \bar{a}_{h} = \frac{a_{hi}}{a_{hk}} $$
2. On soustrait ensuite à chaque autre ligne $j$ la ligne pivot multipliée par le coefficient correspondant de la colonne du pivot $a_{jk}$ : $$ \bar{a}_{j} = a_{j} - a_{jk} \cdot \bar{a}_{h} $$ Cette opération annule tous les autres éléments de la colonne du pivot, à l’exception du pivot lui-même.

Exemple pratique

Considérons la matrice suivante :

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

Choisissons comme pivot l’élément $a_{23}$, c’est-à-dire le troisième élément de la deuxième ligne.

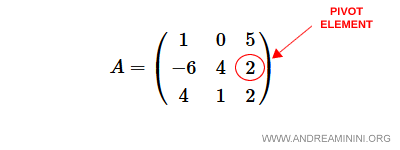
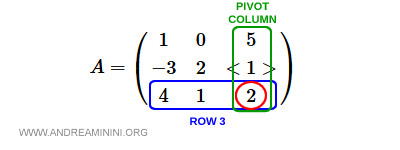
On en déduit que la troisième colonne est la colonne pivot et que la deuxième ligne joue le rôle de ligne pivot.

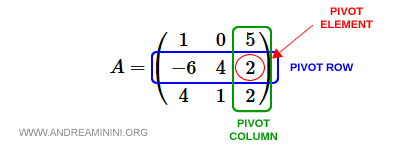
Pour mettre le pivot en évidence, on le souligne à l’aide des symboles <> :

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & <2> \\ 4 & 1 & 2 \end{pmatrix} $$

Divisons maintenant chaque élément de la ligne pivot par le pivot $a_{23} = 2$ :

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ \frac{-6}{2} & \frac{4}{2} & <\frac{2}{2}> \\ 4 & 1 & 2 \end{pmatrix} $$

$$ A = \begin{pmatrix} 1 & 0 & 5 \\ -3 & 2 & <1> \\ 4 & 1 & 2 \end{pmatrix} $$

La ligne pivot est désormais normalisée et le pivot vaut 1.

Nous procédons ensuite à la deuxième étape : soustraire à chaque autre ligne la ligne pivot multipliée par le coefficient correspondant de la colonne du pivot (k = 3).

Ligne 1

La première ligne est $[1, 0, 5]$, avec $5$ en position de pivot.

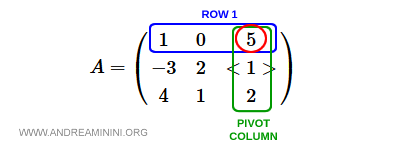
$$ a_1 = [1 \:\: 0 \:\: 5] - 5 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_1 = [1 \:\: 0 \:\: 5] - [-15 \:\: 10 \:\: 5] $$

$$ a_1 = [16 \:\: -10 \:\: 0] $$

Ligne 2

C’est la ligne pivot, elle reste donc inchangée.

Ligne 3

La troisième ligne est $[4, 1, 2]$, avec $2$ dans la colonne du pivot.

$$ a_3 = [4 \:\: 1 \:\: 2] - 2 \cdot [-3 \:\: 2 \:\: 1] $$

$$ a_3 = [4 \:\: 1 \:\: 2] - [-6 \:\: 4 \:\: 2] $$

$$ a_3 = [10 \:\: -3 \:\: 0] $$

À l’issue de cette étape, les première et troisième lignes ont été correctement transformées.

Résultat final

Après avoir appliqué le pivot à $a_{23}$, on obtient la matrice suivante :

$$ A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

Le pivot a été réduit à 1 et tous les autres éléments de sa colonne ont disparu.

Une autre méthode

On peut également utiliser une approche alternative, qui repose sur la construction d’une matrice identité de taille m × m.

Soit une matrice $M$ de dimensions m × n et un pivot $a_{h,k}$. La procédure est la suivante :

1. Construire la matrice identité $Q$ d’ordre m.
2. Remplacer la colonne h de $Q$ par la colonne k de $M$.
3. Remplacer l’élément pivot $a_{h,k}$ de $Q$ par son inverse.
4. Multiplier les autres éléments de la colonne du pivot par l’opposé de cet inverse.
5. Calculer le produit $M' = Q \cdot M$.
6. La matrice $M'$ ainsi obtenue représente l’effet de l’opération de pivot.

Exemple d’application

Appliquons maintenant cette méthode alternative à la matrice $A$ de l’exemple précédent.

La matrice comporte $m=3$ lignes et $n=3$ colonnes, avec pour pivot $a_{2,3} = 2$.

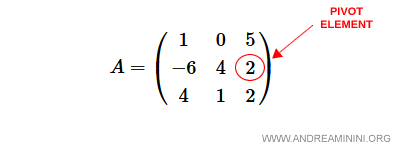
On part de la matrice identité $Q$ (3 × 3) :

$$ Q = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} $$

On remplace la colonne h=2 de $Q$ par la colonne k=3 de $A$, en indiquant le pivot avec <> :

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & <2> & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

Puis on remplace le pivot par son inverse :

$$ Q = \begin{pmatrix} 1 & 5 & 0 \\ 0 & \frac{1}{<2>} & 0 \\ 0 & 2 & 1 \end{pmatrix} $$

On multiplie ensuite les autres éléments de la colonne h=2 par l’opposé de cet inverse :

$$ Q = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} $$

Enfin, on calcule le produit $Q \cdot A$ :

$$ Q \cdot A = \begin{pmatrix} 1 & -\frac{5}{2} & 0 \\ 0 & \frac{1}{2} & 0 \\ 0 & -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 5 \\ -6 & 4 & 2 \\ 4 & 1 & 2 \end{pmatrix} $$

$$ Q \cdot A = \begin{pmatrix} 16 & -10 & 0 \\ -3 & 2 & <1> \\ 10 & -3 & 0 \end{pmatrix} $$

On retrouve exactement le même résultat que par la méthode directe, ce qui confirme la cohérence et la validité de cette approche alternative.