Matrice diagonale
Une matrice carrée est dite diagonale lorsque tous les éléments situés en dehors de la diagonale principale sont nuls.

Autrement dit, si \( i \neq j \), alors \( a_{ij} = 0 \).
Exemple
Considérons, par exemple, une matrice diagonale d’ordre 3, c’est-à-dire comportant trois lignes et trois colonnes.
On constate que tous les éléments placés au-dessus ou en dessous de la diagonale principale sont égaux à zéro.
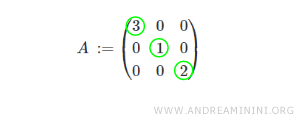
Remarque : Les éléments de la diagonale principale peuvent aussi bien être nuls que non nuls.
De ce fait, une matrice diagonale peut être vue comme un cas particulier de matrice triangulaire supérieure aussi bien que de matrice triangulaire inférieure.

En mathématiques, l’ensemble des matrices diagonales d’ordre \( n \) à coefficients réels se note \( D(n, R) \), où \( n \) désigne l’ordre de la matrice et \( R \) l’ensemble des nombres réels.
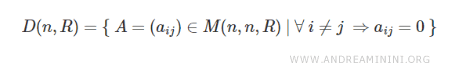
En résumé, les matrices diagonales occupent une place centrale en algèbre linéaire et interviennent dans de nombreuses applications, tant en mathématiques pures que dans les sciences appliquées.