Matrice adjointe
La matrice adjointe est une notion fondamentale de l’algèbre matricielle, largement utilisée dans de nombreux domaines des mathématiques. En termes simples, l’adjointe (également appelée matrice adjointe ou transposée de la comatrice) se définit comme la transposée de la matrice des cofacteurs d’une matrice donnée. Dans les notations courantes, on la désigne par adj.
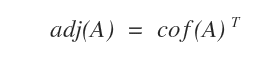
Voyons pas à pas comment se détermine la matrice adjointe.
Considérons la matrice $A$ :
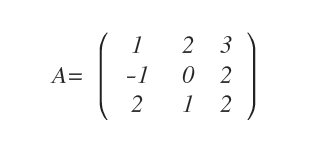
La première étape consiste à construire la matrice des cofacteurs de $A$.
Qu’est-ce qu’un cofacteur ? Les cofacteurs (ou compléments algébriques) se calculent à partir des mineurs des éléments $a_{ij}$ de la matrice $A$, en les multipliant par le signe $(-1)^{i+j}$.
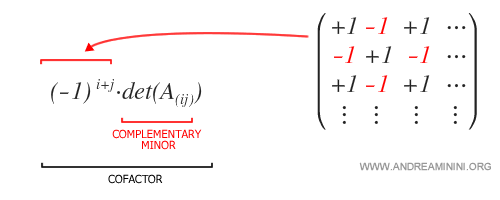
La matrice des cofacteurs, notée $\text{cof}(A)$, est donc :
$$ \text{cof}(A) = \begin{pmatrix} (-1)^{1+1} \, \det(A_{1,1}) & (-1)^{1+2} \, \det(A_{1,2}) & (-1)^{1+3} \, \det(A_{1,3}) \\ (-1)^{2+1} \, \det(A_{2,1}) & (+1) \cdot \det(A_{2,2}) & (-1)^{2+3} \, \det(A_{2,3}) \\ (+1) \cdot \det(A_{3,1}) & (-1)^{3+2} \, \det(A_{3,2}) & (+1) \cdot \det(A_{3,3}) \end{pmatrix} $$
En remplaçant chaque terme par le déterminant de son mineur correspondant, on obtient :
$$ \text{cof}(A) = \begin{pmatrix} -2 & 6 & -1 \\ -1 & -4 & 3 \\ 4 & -5 & 2 \end{pmatrix} $$
La matrice adjointe de $A$ est la transposée de cette comatrice :
$$ \text{adj}(A) = \text{cof}(A)^T = \begin{pmatrix} -2 & -1 & 4 \\ 6 & -4 & -5 \\ -1 & 3 & 2 \end{pmatrix} $$
On a donc obtenu la matrice adjointe de $A$ en prenant simplement la transposée de la matrice des cofacteurs.
La construction de la matrice adjointe intervient dans des contextes essentiels de l’algèbre linéaire : elle permet notamment de calculer l’inverse d’une matrice, de résoudre des systèmes d’équations par la règle de Cramer et d’étudier certaines transformations linéaires dans les espaces vectoriels.