Sous-matrices
Une sous-matrice s’obtient en sélectionnant certaines lignes et certaines colonnes d’une matrice donnée, tout en respectant rigoureusement l’ordre original dans lequel elles apparaissent.

Définition d’une sous-matrice : Soient \( I = \{1, \dots, m\} \) et \( J = \{1, \dots, n\} \) deux ensembles d’indices de \( \mathbb{Z} \), et soit \( A = (a_{ij}) \) une matrice de dimension \( m \times n \), avec \( i \in I \) et \( j \in J \). Si l’on choisit \( H \subseteq I \) et \( K \subseteq J \), la sous-matrice correspondante se note \( A_{HK} = (a_{ij}) \), où \( i \in H \) et \( j \in K \).
Exemple pratique
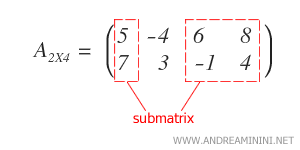
Considérons une matrice \( A_{2 \times 4} \), c’est-à-dire une matrice comportant deux lignes (\( m = 2 \)) et quatre colonnes (\( n = 4 \)).
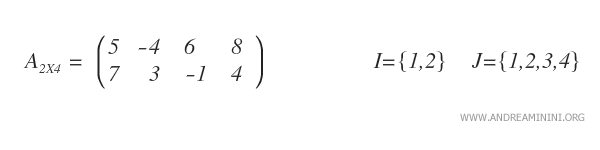
En sélectionnant des sous-ensembles précis \( H \) et \( K \) de \( I \) et \( J \), on obtient une sous-matrice \( A_{HK} \).
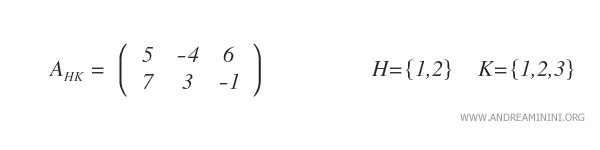
Remarque : Dans ce cas, on a retenu les trois premières colonnes, en omettant la dernière.
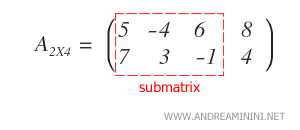
Il convient de noter que les lignes et les colonnes sélectionnées n’ont pas besoin d’être contiguës.
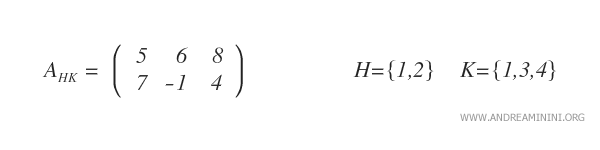
Remarque : Dans cet exemple, la sous-matrice est obtenue en sélectionnant la première, la troisième et la quatrième colonne.
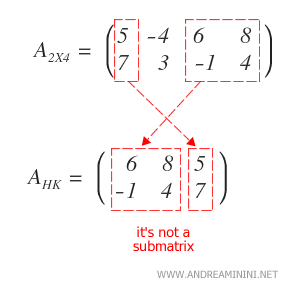
L’essentiel est que la sous-matrice conserve l’ordre relatif des lignes et des colonnes tel qu’il apparaît dans la matrice d’origine.
Exemple : Si l’on modifie l’ordre des colonnes retenues, la matrice obtenue n’est plus une sous-matrice au sens strict, même si elle contient les mêmes valeurs. Elle n’est donc pas considérée comme une sous-matrice valide, car l’ordre des colonnes a été modifié.